La dynamique des populations

Des informations sur la taille et l'âge maximaux des poissons, sur leurs relations longueur-poids, des estimations de leurs paramètres de croissance, de leur mortalité naturelle et de la variabilité de leur recrutement sont cruciales pour des buts de gestion des pêches.

Alors qu'âge et taille maximaux et relations longueur-poids sont relativement faciles à obtenir pour la plupart des espèces de poissons, s'assurer que ces informations soient disponibles à chaque fois qu'elles sont requises, et dans le format approprié, est plutôt plus difficile.

Ce problème est décuplé pour les paramètres de croissance, qui sont plus difficiles à obtenir : ces données correspondent typiquement à celles rapportées dans les mémoires de maîtrise, DEA et thèses, ou dans les courtes notes scientifiques. Pour les séries chronologiques de recrutement, de nombreuses années sont nécessaires pour mettre en évidence des tendances. Ainsi, la recherche sur l'évaluation des stocks peut-elle être accélérée en rendant accessibles aux praticiens des paramètres de croissance qui ont déjà été estimés, soit pour remplacer des évaluations spécifiques par des valeurs pour des stocks avoisinants, soit pour apprécier la validité de ses propres données. Des considérations semblables s'appliquent aux estimations de la mortalité naturelle et aux séries chronologiques de recrutement.

Ces points sont si contraignants pour la recherche halieutique tropicale qu'ils ont fourni une raison suffisante en 1987 pour proposer la création d'une base de données, qui finalement est devenue FishBase : inclure « un résumé des informations sur la croissance et sur la mortalité de chaque espèce […] avec l'objectif ultime de traiter 2 500 espèces. » (Pauly 1988).

Cette prévision sous-estimait le nombre d'espèces à inclure dans FishBase (dix fois plus finalement), mais elle surestimait le nombre d'espèces pour lesquelles des paramètres de croissance et des informations relatives existent : nous avons aujourd'hui répertorié des paramètres de croissance publiés pour environ 1 150 espèces, mais il ne sera pas possible d'atteindre 2 000 espèces pour l'an 2 000. Cependant, les espèces traitées pour l'instant concernent plus de 95 % des captures par pêche mondiales, assurant la pertinence des données entrées dans les tables présentées ci-dessous.

De la même façon, les stocks pour lesquels plus de 600 séries chronologiques de recrutement sont incluses appartiennent aux stocks les mieux étudiés, et à la plupart des stocks monospécifiques d'importance dans le monde.

Plusieurs précautions ont été prises pour assurer la plus grande exactitude possible des données dans les tables précitées. Cela comprend, entre autres, d'écarter des estimations de paramètres incompatibles avec celles réalisées sur la même espèce ou sur des espèces fortement apparentées. Cependant, nous sommes conscients que ces procédures ne peuvent pas identifier toutes les erreurs, ni dans les articles originaux ni pendant la saisie des données. Tout ce que nous pouvons espérer est que vous nous signaliez erreurs et incohérences pour les corriger dans l'édition prochaine de FishBase. Nous traiterons en priorité les cas signalés ‹ hors limites › (‹ Out of range ›) dans le champ Remarks qui font référence à des travaux conduits en-dehors de l'aire de répartition de l'espèce étudiée, suggérant ainsi une erreur d'identification.

Les informations sur la dynamique des populations peuvent être imprimées :

• par famille ou par pays, en utilisant des rapports prédéfinis accessibles par la fenêtre MAIN MENU ;
• par espèce à partir des tables respectives ;
• intégrés à un synopsis d'espèce.

Référence

Pauly, D. 1988. Resource assessment and management program, p. 47-66. In ICLARM five-year plan (1988-1992), Part 1. directions and opportunities. International Center for Living Aquatic Resources Management (ICLARM), Manila.

Daniel Pauly et Crispina Binohlan

La table POPCHAR

Cette table présente des informations sur la longueur (Lmax), le poids (Wmax) et l'âge (tmax) maximaux pour plusieurs localités où une espèce est présente. Les valeurs les plus grandes de cette table sont aussi entrées dans la table SPECIES. La table POPCHAR indique aussi si les valeurs de Lmax, Wmax et tmax, ou diverses combinaisons, font référence au même spécimen.

La table contient environ 1 500 enregistrements pour plus de 700 espèces, extraits de plus de 400 références.

Les utilisateurs de FishBase peuvent considérer cette table comme notre réponse au Livre Guinness des Records 2000 (Anon, sous presse). Nous envisageons de nombreuses directions d'utilisation de ces données, par exemple pour tester des hypothèses issues des théories biologiques.

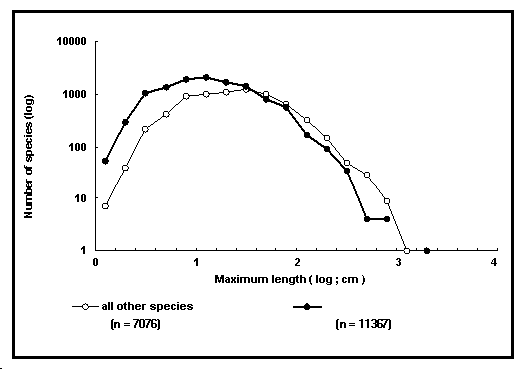
Fig. 14. Distribution de la longueur des poissons tropicaux en comparaison avec les autres espèces dans FishBase.

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population dynamics dans la vue BIOLOGY, puis sur le bouton Maximum Sizes dans la fenêtre POPULATION DYNAMICS.

Référence

Anon. Le livre Guinness des Records 2000. Guinness Media (sous presse).

Crispina Binohlan et Daniel Pauly

La table LENGTH-WEIGHT

Les relations longueur-poids sont importantes en halieutique, particulièrement pour inférer les distributions de fréquences dans les captures totales à partir d'échantillons, ou pour estimer la biomasse à partir d'évaluations sous-marines des longueurs. La table LENGTH-WEIGHT présente les valeurs des constantes a et b pour plus de 4 000 relations longueur-poids de la forme W = a  Lb, se rapportant à 1 700 espèces de poissons environ.

Cependant, les relations longueur-poids publiées sont parfois difficiles à utiliser, car elles peuvent être fondées sur un type de longueur (par exemple, la longueur à la fourche) différent de celui de la longueur utilisée pour autre chose (par exemple, la longueur totale pour la croissance).

Par conséquent, pour faciliter la conversion entre différents types de longueur, une table supplémentaire LENGTH-LENGTH, présentée ci-dessous, a été conçue. Elle contient des régressions linéaires ou des ratios reliant les différents types de longueur (par exemple, LF en fonction de LT).

Sources

Les relations longueur-poids ont été extraites de 1 100 références environ, par exemple, Carlander (1969, 1977) ; Cinco (1982) ; Dorel (1985) ; Bohnsack et Harper (1988) ; Coull et al. (1989) ; Torres (1991) ; et Kulbicki et al. (1993).

Les champs

Un champ calculé contient le poids d'un poisson de 10 cm (qui devrait être de l'ordre de 10 g pour un poisson ‹ normal ›, fusiforme), pour permettre le repérage d'erreurs manifestes, la forme du corps étant connue. De plus, cliquer sur le bouton ‹ graphique › dans la table sommaire, affiche des courbes longueur-poids (Fig. 15). Cette procédure peut être utilisée pour repérer des courbes qui dévient de la tendance générale.

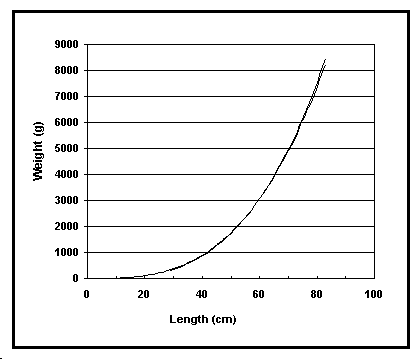
Fig. 15. Les deux relations longueur-poids actuellement disponibles dans FishBase pour Lutjanus bohar. Noter que vous pouvez utiliser ce graphique pour estimer un poids en fonction d'une longueur donnée.

Un champ à choix multiple indique la méthode utilisée pour l'estimation des paramètres a et b des relations longueur-poids parmi les méthodes suivantes :

1. Régressions linéaires de type I (ou ‹ prédictif ›) de logW en fonction de logL (la méthode choisie dans la majorité des cas) ;
2. Régression linéaire de type II (ou ‹ fonctionnel ›) de logW en fonction de logL (comme suggéré par Ricker 1980, mais rarement utilisée, car les relations longueur-poids sont généralement exploitées pour prédire W, L étant connu) ;
3. Comme (1) ou (2), mais avec correction des erreurs systématiques comme suggéré par Sprugel (1983 ; voir aussi Vakily et al. 1986) ;
4. Régression non-linéaire de W en fonction de L, comme recommandé par Saila et al. (1988) par exemple ;
5. Algorithme de Pauly et Gayanilo (1996), à partir de distributions de fréquences des longueurs et du poids des spécimens groupés par classe de longueur ;
6. Calcul de la constante a avec un seul couple de valeurs L-W pour b = 3 ;
7. Calcul de la constante a en utilisant les moyennes géométriques des valeurs L et W, ou en prenant la moyenne des valeurs a calculées pour chaque couple de valeurs L-W, pour b = 3 ;
8. Toute autre méthode (par exemple, celle de Lenarz 1994, telle que spécifiée dans le champ Comment).

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population dynamics dans la vue BIOLOGY, puis sur le bouton L-W relationship dans la fenêtre POPULATION DYNAMICS. Le nom interne de cette table est POPLW.

Références

Bohnsack, J.A. et D.E. Harper. 1988. Length-weight relationships of selected marine reef fishes from the southeastern United States and the Caribbean. NOAA Tech. Mem. NMFS-SEFC-215, 31 p.

Carlander, K.D. 1969. Handbook of freshwater fishery biology. Tome. 1. The Iowa State University Press, Ames, Iowa. 752 p.

Carlander, K.D. 1977. Handbook of freshwater fishery biology. Tome. 2. The Iowa State University Press, Ames, Iowa. 431 p.

Cinco, E. 1982. Length-weight relationships of fishes, p. 34-37. In D. Pauly et A.N. Mines (éds.). Small-scale fisheries of San Miguel Bay : biology and stock assessment. ICLARM Tech. Rep. 7, 124 p.

Coull, K.A., A.S. Jermyn, A.W. Newton, G.I. Henderson et W.B. Hall. 1989. Length-weight relationships for 88 species of fish encountered in the North Atlantic. Scottish Fish. Res. Rep. 43, 80 p.

Dorel, D. 1985. Poissons de l'Atlantique nord-est : relations taille-poids. Institut Français de Recherche pour l'Exploration de la Mer, Paris. 165 p.

Kulbicki, M., G. Mou Tham, P. Thollot et L. Wantiez. 1993. Length-weight relationships of fish from the lagoon of New Caledonia. Naga, ICLARM Q. 16(2-3) : 26-29.

Lenarz, W.H. 1994. Estimation of weight-length relationship from group measurements. US Fish. Bull. 93 : 198-202.

Pauly, D. et F.C. Gayanilo, Jr. 1996. Estimating the parameter of length-weight relationship from length-frequency samples and bulk weights, p. 136. In D. Pauly et P. Martosubroto (éds.). Baseline studies of biodiversity : the fish resources of western Indonesia. ICLARM Stud. Rev. 23, 321 p.

Ricker, W.E. 1980. Calculs et interprétation des statistiques des populations de poissons. Bull. Fish. Res. Board Can. 191F, 409 p.

Saila, S.B., C.W. Recksiek et M.H. Prager. 1988. Basic fishery science programs : a compendium of microcomputer programs and manual of operation. Elsevier Science Publishing Co., New York. 230 p.

Sprugel, D.G. 1983. Correcting for bias in log-transformed allometric equations. Ecology 64(1) : 209-210.

Torres, F. Jr. 1991. Tabular data on marine fishes from Southern Africa, Part I. Length-weight relationships. Fishbyte 9(1) : 50-53.

Vakily, J.M., M.L. Palomares et D. Pauly. 1986. Computer programs for fish stock assessment: applications for the HP41 CV calculator. FAO Fish. Tech. Pap. 101 Suppl. 1, 255 p. Rome.

Crispina Binohlan et Daniel Pauly

La table LENGTH-LENGTH

Cette table contient des facteurs de conversion d'un type de longueur en un autre pour environ 2 000 espèces de poissons, extraits de 170 publications différentes environ ou d'illustrations. Les facteurs sont calculés avec des longueurs exprimées en centimètres, soit sous la forme d'une régression :

Longueur type (2) = a + b Longueur type (1) …1)

soit sous la forme d'un ratio b', c'est-à-dire

Longueur type (2) = b' Longueur type (1) …2)

Les types de longueur disponibles sont, comme ailleurs dans FishBase,

LT = longueur totale ;

FL = longueur à la fourche ;

LS = longueur standard ;

WD = largeur du disque (chez les raies) ;

OT = autre type (tel que spécifié dans le champ Comment).

Avec les équations de type (1) sont indiqués l'intervalle des longueurs, le nombre et le sexe des poissons utilisés pour le calcul de la régression, ainsi que le coefficient de corrélation.

Avec les équations de type (2) sont omis l'intervalle des longueurs et le coefficient de corrélation car le ratio aura généralement été estimé à partir d'un ou quelques spécimens de longueur similaire.

Les sources sont indiquées dans les deux cas par le champ MainRef. ou, pour les ratios, par une référence à une ou plusieurs illustrations.

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population dynamics dans la vue BIOLOGY, puis sur le bouton L-L relationship dans la fenêtre POPULATION DYNAMICS. Le nom interne de cette table est POPLL.

Crispina Binohlan, Rainer Froese et Daniel Pauly

La table POPGROWTH

Cette table contient des informations sur la croissance, la mortalité naturelle et la longueur à maturité, qui servent de paramètres à de nombreux modèles d'évaluation des stocks de poissons. Les données peuvent aussi être utilisées pour établir des relations empiriques entre des paramètres de croissance ou des valeurs de mortalité naturelle estimées, et d'autres paramètres (par exemple, la forme du corps, la température, etc.). C'est une voie de recherche utile pour l'évaluation des stocks et pour comprendre de mieux en mieux l'évolution des stratégies de vie (voir Fig. 16).

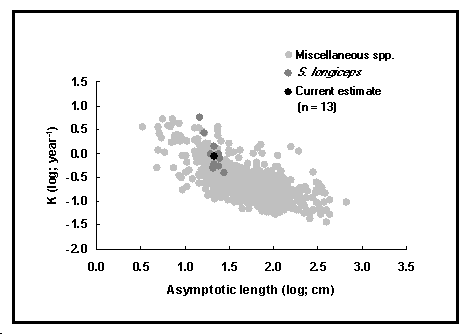
Fig. 16. Nuage auximétrique chez Sardinella longiceps et de 20 % des données chez d'autres espèces.

Les paramètres de croissance contenus dans cette table sont ceux de la courbe de von Bertalanffy (CVB ; von Bertalanffy 1938), qui s'exprime pour la croissance en longueur :

...1)

où Lt est la longueur moyenne prédite pour un individu d'une population donnée à l'âge t, L, leur longueur asymptotique moyenne, c'est-à-dire la longueur qu'ils atteindraient à un âge infini, K, un coefficient de croissance de dimension temps-1, et t0, l'âge théorique (et généralement négatif) pour une longueur nulle, obtenu par extrapolation de la CVB.

Corrélativement, la CVB s'exprime pour la croissance en poids :

...2)

où Wt et W sont les poids correspondant respectivement aux Lt et L, et b, le coefficient extrait d'une relation longueur-poids de type :

W = a ...3)

POPGROWTH contient des enregistrements pour lesquels au moins L et K sont disponibles ; t0 peut être absent (ce paramètre non-biologique n'est pas requis dans la plupart des modèles d'évaluation des stocks).

Sources

Approximativement, la table contient actuellement 4 700 jeux de paramètres de croissance estimés pour 1 150 espèces, extraits de 2 000 sources primaires et secondaires. Les compilations de Pauly (1978, 1980) constituent un tiers de ces enregistrements environ.

Les champs

En plus du champ MainRef., un champ Ref. est associé à chaque ensemble de paramètres de croissance, car dans les articles, ils sont souvent publiés sans les données qui ont servi à leur calcul. Les données sources sont indiquées parmi les choix suivants : annuli d'otolithe ; annuli d'écaille ; autres marques annuelles ; anneaux d'otolithe journaliers ; marquage/recapture ; distribution de fréquences de longueur ; observation directe ; plusieurs types de données ; autres.

La méthode utilisée pour chaque ensemble de paramètres de croissance estimés est indiquée parmi les choix suivants : droite de Ford-Walford ; droite de von Bertalanffy/Beverton ; droite de Gulland et Holt ; régression non-linéaire ; ELEFAN ; autre(s) méthode(s).

Des descriptions de ces méthodes, de leurs hypothèses sous-jacentes, de la conformité des données et de leurs biais peuvent être trouvées dans Bougis (1976), Ricker (1980), Gulland (1983), Pauly (1984 ; 1997), Gayanilo et Pauly (1997), et d'autres publications halieutiques.

Les champs suivants permettent de vérifier sommairement l'exactitude des paramètres de croissance :

a. un champ calculé contient l'indice de performance de croissance ø' = log10K + 2log10L (Pauly 1979 ; Pauly et Munro 1984 et voir ‹ Analyses Auximétriques ›, ce volume), qui peut être comparé avec les valeurs du ø' de stocks de la même espèce ou d'une espèce étroitement apparentée ;

b. un champ à choix multiples indique la méthode de calcul de W en fonction de L parmi les choix suivants :

1. Comme indiquée dans MainRef. ou Ref. pour la croissance ;
2. Calcul par rel. L/W du même stock ;
3. Calcul par rel. L/W d'un stock différent de la même espèce ;
4. Calcul par rel. L/W d'une espèce similaire ;
5. Autres (voir Comments).

c. un champ oui/non indique les cas où L est différent de Lmax (dans la table SPECIES) de plus de 30 % de Lmax ;

d. quand plus de 4 enregistrements sont disponibles, un champ indique si le couple de valeurs W-K se situe en dehors de l'ellipse auximétrique (voir ‹ Analyse Auximétrique ›, ce volume) définie par les autres couples W - K pour l'espèce en question ;

e. cliquer sur le bouton ‹ graphique › Growth curves dans la table sommaire affiche les courbes de la longueur en fonction de l'âge relatif (= âge réel - t0) (Fig. 17). Cette procédure peut être utilisée pour repérer des courbes de croissance qui dévient de la tendance générale ;

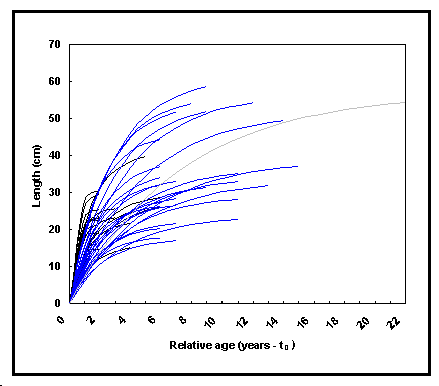
Fig. 17. Longueur en fonction de l'âge relatif (t-t0) pour Oreochromis niloticus niloticus. Ces courbes sont calculées par application de la CVB (Équation 1) aux paramètres L et K de la table POPGROWTH. Les courbes de croissance à asymptote faible correspondent plutôt à des croissances en captivité (voir Encadré 15 et Fig. 18).

f. cliquer sur les deux boutons ‹ graphique › suivant affiche des courbes auximétriques, correspondant respectivement à logK en fonction de logL (voir Fig. 16) et de W (voir ‹ Analyses Auximétriques ›, ce volume) ;

g. un champ indique si l'ensemble des paramètres de croissance ont été mesurés sur des individus vivant en ‹ eaux libres › ou en ‹ captivité › (voir Encadré 15 et Fig. 18).

Les informations sur la longueur à maturité (Lm), contenues dans une table séparée (MATURITY), sont utilisées ici conjointement avec L pour calculer le ‹ fardeau reproductif › (Cushing 1981) de la population, c'est-à-dire le rapport Lm/L. La plupart des valeurs Lm correspondent à une longueur moyenne ou à la longueur à laquelle 50% de la population est mature. Mais quand ces valeurs n'ont pas été précisées dans les publications, ou ne peuvent pas être calculées à partir des données, Lm est la moyenne des deux valeurs limites.

Pour quelques enregistrements, les estimations de L restent à comparer avec la longueur maximale enregistrée (Lmax) qui devrait en être a priori raisonnablement proche (voir ci-dessus).

Nous attendons les commentaires des utilisateurs sur le contenu et/ou l'utilité de la table POPGROWTH avec impatience.

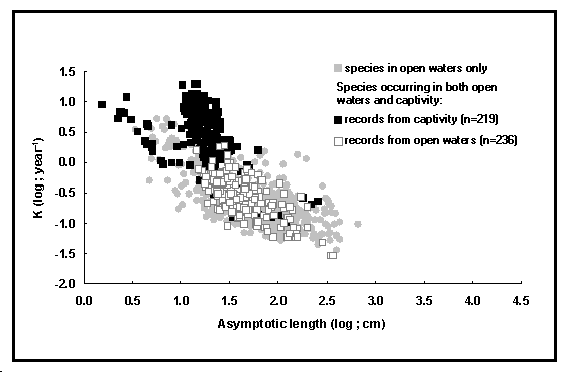
Fig. 18. Nuage auximétrique visualisant la croissance des poissons en captivité. Les carrés noirs dont le log(L) est compris entre 1,0 et 1,5 correspondent principalement à des Oreochromis niloticus élevés en systèmes intensifs et semi-intensifs (voir Encadré 15).

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population dynamics dans la vue BIOLOGY, puis sur le bouton Growth dans la fenêtre POPULATION DYNAMICS. La Fig. 18 s'obtient aussi en cliquant sur le bouton Reports dans la fenêtre MAIN MENU puis sur le bouton Population dynamics dans la fenêtre GRAPHS MENU.

Références

Bougis, P. Éditeur. 1976. Océanographie biologique appliquée : l'exploitation de la vie marine. Masson, Paris, 320 p.

Cushing, D.H. 1981. Fisheries biology : a study in population dynamics. 2nd édition. University of Wisconsin Press, Madison. 295 p.

Gayanilo, F.C., Jr et D. Pauly. 1997. The FAO-ICLARM Stock Assessment Tool (FiSAT). Reference Manual. FAO Comp. Inf. Ser./Fish. 8, 262 p.

Gulland, J.A. 1983. Fish stock assessment : a manual of basic methods. FAO/Wiley, Chichester, New York. 223 p.

Pauly, D. 1978. A preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 55, 200 p.

Pauly, D. 1979. Gill size and temperature as governing factors in fish growth : a generalization of von Bertalanffy's growth formula. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 63, 156 p.

Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. CIEM 39(2) : 175-192.

Pauly, D. 1984. Fish population dynamics in tropical waters : a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.

Pauly, D. 1997. Méthodes pour l'évaluation des ressources halieutiques. Collection Polytech. Cépaduès Editions, Toulouse, 288 p.

Pauly, D. et J.L. Munro. 1984. Once more on growth comparison in fish and invertebrates. Fishbyte 2(1) : 21.

Ricker, W.E. 1980. Calculs et interprétation des statistiques des populations de poissons. Bull. Fish. Res. Board Can. 191F, 409 p.

von Bertalanffy, L. 1938. A quantitative theory of organic growth. (Inquiries on growth laws II). Hum. Biol. 10 : 181-213.

Crispina Binohlan et Daniel Pauly

Les analyses auximétriques

Pendant le processus de croissance des poissons, la taille (exprimée par un poids ou une longueur) varie au cours du temps. Toute tentative de représenter ou de comparer des croissances doit traiter ces deux dimensions. Cependant, comparer les courbes de croissance, qui relient la taille au temps, n'est pas simple. En effet, selon la définition acceptée des croissances ‹ lente › et ‹ rapide ›, de sérieuses contradictions surgissent quand des courbes de croissance se croisent. Aussi Kinne (1960) écrit-il que « la différence de taux de croissance établis chez de jeunes poissons ne persiste pas tout au long de la vie. Les poissons à croissance initiale lente peuvent surpasser des poissons à croissance initiale rapide, et finalement atteindre une longueur supérieure à âge égal. » (Ce phénomène est bien illustré par la Fig. 17).

Dans FishBase, nous utilisons les paramètres de la courbe de von Bertalanffy ou CVB (voir ‹ La table POPGROWTH ›, ce volume) pour décrire la croissance des poissons. Cependant, cela ne résout pas en soi le problème posé par Kinne (1960), car aucun de ces paramètres n'a une dimension de croissance (c'est-à-dire, unité de longueur ou de poids par unité de temps). L et W ne représentent que la taille, et K et t0 que le temps (temps-1 et temps, respectivement). Cependant, des combinaisons variées de ces paramètres, par exemple L·K, ont des dimensions appropriées (ici : longueurtemps-1), c'est-à-dire celle d'un taux de croissance (Gallucci et Quinn 1979). Bien qu'utilisant des logarithmes, les indices de performance de croissance :

•  = logK + 2logL …1)

et

•  = logK + (2/3)logW …2)

ont aussi une dimension correcte de taux de croissance, et sont maintenant largement utilisés pour comparer les performances de croissance des différents poissons et des invertébrés, considérant les distributions normales (et relativement étroites) des différentes populations d'une même espèce (voir, par exemple, Moreau et al. 1986). Cette dernière caractéristique permet aussi l'estimation de K à partir de L ou W quand leur Ø' ou Ø (moyens) est connu d'une (de plusieurs) population(s) (Munro et Pauly 1983 ; Pauly et Munro 1984).

Les pentes de 2 et 2/3 respectivement dans les équations (1) et (2) ont été estimées par Pauly (1979) à partir d'un grand ensemble de données maintenant inclus dans FishBase (Pauly 1978, 1979). L'équation (1) implique que les courbes de logK en fonction de logL auront une pente de -2 en moyenne, et l'équation (2), que les courbes de logK en fonction de logW auront une pente de -2/3.

Un nuage ‹ auximétrique › (des mots grecs pour ‹ croissance › et ‹ mesure ›) est un graphique logarithmique du paramètre K de la CVB en fonction de la taille asymptotique (L ou W). Dans cette représentation, une population avec son ensemble de paramètres de croissance (L -K ou W -K) est représentée par un seul point, et les différentes populations de la même espèce auront tendance à être regroupées. Comme les équations (1) et (2) impliquent que ces groupes doivent s'aligner le long de droites de régression de pente connue, ils peuvent être superposées par des ellipses dont le grand axe présente également une pente égale à 2 ou 2/3, dont les points d'intersection sont égaux à Ø' ou Ø, et dont les surfaces correspondent à la variance des ensembles de valeurs qu'ils représentent.

Les ellipses d'une surface égale aux 95% de limite de confiance (S95) d'un groupe de couples L-K (ou W-K) peuvent donc être estimées facilement. Le logiciel AUXIM (Pauly et al. 1996) calculent des S95 pour des groupes d'au moins 4 couples L -K ou W-K, et dispose de routines associées.

Comme AUXIM serait fastidieux à utiliser séparément, un sous-ensemble de ses routines a été inclus dans FishBase 99 pour permettre l'analyse du grand nombre de paramètres de croissance qui y sont disponibles. Néanmoins, pour permettre des comparaisons entre des poissons de conformation très différentes, seules les routines qui se rapportent à la croissance en poids (et à Ø, pas à Ø') ont été incluses. De plus, seuls les poissons vivant en eaux libres (et pas ceux en captivité) peuvent être inclus dans les analyses (la raison en est donnée dans l’Encadré 15).

Comment y arriver

Les analyses auximétriques sont appelées de la fenêtre REPORTS, après avoir identifié un groupe d'espèces (par environnement ou par taxon supra-spécifique, ordre, famille ou genre). Une analyse auximétrique complète comprend :

a) affichage d'un graphique où sont tracées toutes les ellipses par espèce sélectionnée ayant au moins 4 données (voir Fig. 19 ; Encadré 16), et affichage des estimations des valeurs moyennes de K et W ;

b) estimation et affichage sous forme de tableau des distances et des chevauchements entre espèces (pour un minimum de 4 espèces) ; et

c) application de l'algorithme d'agglomération de McCammon et Wenninger (1970) aux distances calculées en (b) pour construire un dendrogramme dans ‹ l'espace de croissance ›, et ainsi montrer les similarités de croissance entre les espèces du groupe sélectionné (Fig. 19).

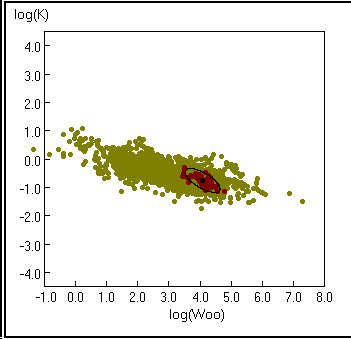
Fig. 19. Courbe de K en fonction de W. Les points clairs représentent toutes les espèces pour lesquelles W est disponible dans FishBase, les points sombres représentent des enregistrements pour Gadus morhua. L'ellipse, avec un point noir en son centre, représente les 95 % de limite de confiance. Voir Encadré 16 pour les détails.

Des analyses telles que celles-ci n'ont été exécutées que pour les tilapias, famille des Cichlidae (Pauly et al. 1996) et les vivaneaux, famille des Lutjanidae (Pauly et Binohlan 1996). Leur potentiel n'a donc pas été complètement exploré. Nous sommes cependant confiants que de telles analyses étendront considérablement la compréhension de la croissance, et plus généralement, de la biologie des poissons. Nous attendons les réactions des utilisateurs avec impatience.

Encadré 16. L'origine et l'utilisation d'AUXIM.

Ce texte, dont la première partie est adaptée de Pauly et al. (1996), résume les caractéristiques essentielles de l'approche utilisées dans AUXIM pour calculer les ellipses. Étant donné le poids CVB, et la définition de Ø, nous avons

logK = Ø - 2/3 logW

qui est l'équation du grand axe de l'ellipse, Ø étant le point d'intersection à l'ordonnée.

Nécessairement puisqu'il est perpendiculaire, l'équation pour le petit axe est

logK = Yo + 3/2 logW

où Yo est l'ordonnée du point d'intersection avec l'axe des ordonnées. L'abscisse du point d'intersection de l'axe mineur avec l'axe des abscisses est

Xo = logW - 2/3 logK

Si une ellipse doit faire référence aux 95% de limite de confiance d'un nuage des points, la longueur (2 . a) du grand axe doit être en rapport avec l'écart-type de Xo ; de même, la longueur du petit axe (2 . b) doit être en rapport avec l'écart-type de Ø, soit

a = t · sd(Xo) · (3/2) · (1 / ((1 + (3/2)2)1/2)

b = t · sd(Ø) · (3/2) · (1/ ((1 + (3/2)2)1/2)

où la valeur de t dépend du nombre de points (n), avec t = 1,96 quand n = (Sokal et Rohlf 1995), et où le facteur (3/2) · (1/ ((1 + (3/2)2)1/2) prend en compte le fait que les axes des ellipses ne sont pas parallèles aux axes du système de coordonnées.

Quand les ellipses font référence à l'écart-type des valeurs moyennes de logW et logK, sd(Xo) et sd(Ø) sont remplacés par les erreur-standard, c'est-à-dire, respectivement par se(Xo) et se(Ø).

Comment utiliser AUXIM :

L'interface utilisateur d'AUXIM se divise en quatre parties :

1. Les boutons de commandes au coin supérieur gauche de l'écran servent à : (i) augmenter ou diminuer la taille de la courbe auximétrique (c'est-à-dire zoom-avant ou zoom-arrière) ; (ii) ouvrir la liste d'espèces sélectionnée avant l'activation de la routine principale d'AUXIM (cliquer sur le bouton Reports dans la fenêtre MAIN MENU, puis sur le bouton Graphs, puis sur le bouton Population Dynamics, puis sur le bouton Auximetric analysis).

2. Affichage des espèces sélectionnées et des boutons permettant le défilement de la liste (coin supérieur droit de l'écran).

3. Affichage de la courbe auximétrique visualisant aussi le tableau des distances et des chevauchements, et le dendrogramme.

4. Les boutons du système de commandes pour : (i) sélectionner ou désélectionner une espèce de la liste ; (ii) imprimer l'affichage courant ou le sauvegarder dans un fichier imprimable ; (iii) ouvrir le fichier d'aide ; ou (iv) fermer la fenêtre et retourner à FishBase.

Noter que les fonctions associées aux boutons de commande sont accessibles en cliquant le bouton droit de la souris. De plus, une espèce peut être sélectionnée ou désélectionnée dans la liste soit en double-cliquant sur l'espèce, soit en tapant la barre d'espacement.

Références

Pauly, D., J. Moreau et F.C. Gayanilo, Jr. 1996. Une nouvelle méthode de comparaison des performance de croissance des poissons, appliquée aux tilapias sauvages et d'élevage, p. 477-485. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (éds). Le Troisième Symposium International sur le Tilapia en Aquaculture. ICLARM Conf. Proc. 41. [Disponible p. 433-441 dans la version anglaise].

Sokal, R.R. et F.J. Rohlf. 1995. Biometry. 3ème Édition. W.H. Freeman and Company, San Francisco. 887 p.

Daniel Pauly et Felimon C. Gayanilo, Jr.

Fig. 20. Dendrogramme des similarités (axe-X en unités arbitraires) dans ‹ l'espace de croissance › défini par AUXIM pour des Gadidae, avec 1 = Theragra chalcogramma ; 2 = Trisopterus luscus ; 3 = Merlangius merlangus ; 4 = Micromesistius poutassou ; 5 = Melanogrammus aeglefinus ; 6 = Gadus morhua ; 7 = Pollachius virens ; 8 = Trisopterus minutus. Comme il peut être constaté, Theragra chalcogramma et Trisopterus luscus d'une part, et G. morhua et P. virens d'autre part, forment 2 groupes bien séparés, les autres espèces s'agglomérant successivement.

Références

Gallucci, V.F. et T.J. Quinn, II. 1979. Reparameterizing, fitting, and testing a simple growth model. Trans. Am. Fish. Soc. 108(1) : 14-25.

Kinne, O. 1960. Growth, food intake, and food consumption in an europlastic fish exposed to different temperatures and salinities. Physiol. Zool. 33 : 288-317.

McCammon, R.B. et G. Wenninger. 1970. The dendrograph. Computer Contribution 48. State Geological Survey. The University of Kansas, Lawrence. 26 p.

Moreau, J., C. Bambino et D. Pauly. 1986. A comparison of four indices of overall fish growth performance, based on 100 tilapia populations (Fam. Cichlidae), p. 201-206. In J.L. Maclean, L.B. Dizon et L.V. Hosillos (éds.). The First Asian Fisheries Forum. Asian Fisheries Society, Manila, Philippines.

Munro, J.L. et D. Pauly. 1983. A simple method for comparing the growth of fishes and invertebrates. Fishbyte 1(1) : 5-6.

Pauly, D. 1978. A preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 55, 200 p.

Pauly, D. 1979. Gill size and temperature as governing factors in fish growth : a generalization of von Bertalanffy's growth formula. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 63, 156 p.

Pauly, D. et J.L. Munro. 1984. Once more on the comparison of growth in fish and invertebrates. Fishbyte 2(1) : 21.

Pauly, D. et C. Binohlan. 1996. FishBase and AUXIM as tools for comparing the life-history patterns, growth and natural mortality of fish : applications to snappers and groupers, p. 223-247. In F. Arreguin-Sánchez, J.L. Munro, M.C. Balgos et D. Pauly (éds.). Biology, fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. 48.

Pauly, D., J. Moreau et F.C. Gayanilo, Jr. 1996. Une nouvelle méthode de comparaison des performance de croissance des poissons, appliquée aux tilapias sauvages et d'élevage, p. 477-485. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (éds). Le Troisième Symposium International sur le Tilapia en Aquaculture. ICLARM Conf. Proc. 41. [Disponible p. 433-441 dans la version anglaise].

Daniel Pauly, Jacques Moreau et Felimon C. Gayanilo, Jr.

La croissance saisonnière

Que la croissance des poissons présente des oscillations saisonnières était bien connu des pionniers de la biologie des pêches, particulièrement de T.W. Fulton (1901, 1904) qui a inventé l'analyse des fréquences de longueur avec C.G.J. Petersen.

Cette connaissance est cependant passée au second plan lorsque les halieutes ont graduellement abandonné l'analyse des longueurs au profit de l'étude des annulis (sur les otolithes, les écailles et les autres os) pour estimer des taux et tracer des courbes de croissance (Went 1972). Ainsi, dans leur classique ouvrage de 1957, Beverton et Holt n'ont pas traité les oscillations saisonnières de croissance au-delà d'une simple curiosité académique, et en particulier, ils n'ont trouvé aucune raison de modifier l'équation de la courbe de von Bertalanffy (CVB) pour rendre compte de telles oscillations, bien qu'elles se produisent chez tous les poissons qu'ils aient étudiés.

Après que von Bertalanffy et Müller aient évoqué la croissance saisonnière en 1943, Ursin fut le premier à publier une CVB qui prenne en compte ces oscillations (1963a, 1963b). D'autres modifications ont ensuite été proposées (Pitcher et MacDonald 1973 ; Daget et Écoutin 1976), bientôt suivies par une succession d'améliorations de ces modèles (Cloern et Nichols 1978 ; Pauly et Gaschütz 1979 ; Appeldoorn 1987 ; Somer 1988 ; Soriano et Pauly 1989). Les exemples d'application présentés par ces auteurs ont mis clairement en évidence que les modèles de croissance qui ne considèrent pas explicitement les oscillations saisonnières omettent un aspect essentiel du processus de croissance (Pauly 1990, 1994).

De plus, même en milieu tropical, la faible différence de température de 2C entre hiver et été suffit à induire des oscillations saisonnières de croissance qui restent statistiquement significatives bien que visuellement indétectables (Pauly et Ingles 1981 ; Longhurst et Pauly 1987).

Le modèle de croissance qui rende compte au mieux des oscillations saisonnières de croissance est probablement celui de Somer (1988), dont l'expression est

Lt = L {1 – exp – [ K (t – t0) + S(t) – S(t0)]} …1)

où

L, K et t0 sont définis comme dans la CVB standard ;

S(t) = (C . K/2) Sin (t – ts) ; et

S(t0) = (C . K/2) Sin (t0 - ts).

L'équation (1) a deux paramètres de plus que la CVB standard : C et ts. C exprime l'amplitude des oscillations de croissance et est le plus facile à interpréter. Quand C = 0, l'équation (1) devient la CVB standard ; quand C = 0,5, les oscillations saisonnières de croissance sont telles que la croissance est augmentée de 50 % au moment du pic de croissance en été, et, brièvemement, réduite de 50% en hiver. Quand C = 1, la croissance varie de 100 %, c'est-à-dire qu'elle double en été, et devient nulle en plein hiver (voir Fig. 21).

Le second nouveau paramètre, ts, correspond à la durée entre t = 0 et le début d'une oscillation sinusoïdale de croissance. Pour se le représenter, il est utile de définir un ‹ point hivernal › (ou Winter Point) WP = ts + 0,5 qui exprime la période de l'année où la croissance est la plus lente. WP est souvent proche de 0,1 dans l'hémisphère nord (c'est-à-dire mi-février) et de 0,6 dans l'hémisphère sud (mi-août), d'où son nom. [Noter que l'alternance de températures estivales hautes et hivernales basses n'est pas nécessairement la cause des oscillations saisonnières de croissance ; chez les poissons d'eau douce de l'Amazone par exemple, ces oscillations sont dues à l'alternance des saisons d'inondation et des saisons sèches. Noter aussi que l'équation (1) ne peut pas décrire de longues périodes de croissance nulle (ni utiliser des valeurs de C > 1), problème discuté par Pauly et al. (1992)].

Comme ce modèle et ses prédécesseurs (particulièrement le modèle de Pauly et Gaschütz 1979) ont été adaptés à de nombreuses données d'oscillations saisonnières de croissance, des évaluations de C sont disponibles pour une large gamme d'espèces et d'habitats.

La table POPGROWTH inclut la plupart des évaluations de C publiées pour les poissons, assorties des évaluations de la différence de température été-hiver (T ; différence des valeurs mensuelles moyennes, en C). Comme il peut être constaté sur la figure 22, ces valeurs de C augmentent avec T, pour un valeur de C proche de 1 quand T est environ de 10C.

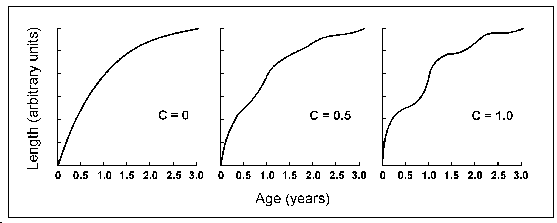
Fig. 21. Effet du paramètre d'amplitude C sur une courbe de von Bertalanffy avec L = 25 unités, K = 1 ans-1, t0 = 0 et ts = 0.

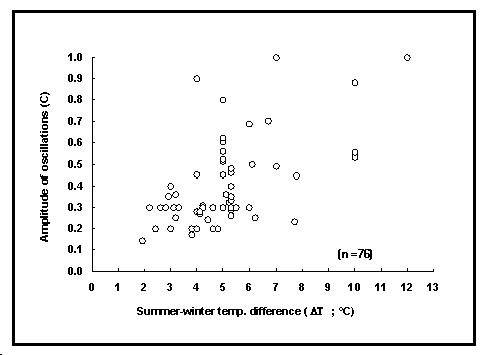
Fig. 22. Relation entre le paramètre C et les différences de température été-hiver de leur habitat (T en C) pour 72 populations de poissons. C reflète l'amplitude des oscillations saisonnières de croissance.
Quelques-unes des implications physiologiques de cette relation sont connues depuis le début des années 1980 (voir par exemple, Pauly et Ingles 1981), et sont discutées par Longhurst et Pauly (1987).

Comment y arriver

Pour afficher le graphique de la figure 22, cliquer sur le bouton Reports dans la fenêtre MAIN MENU, puis sur le bouton Graphs dans la fenêtre PREDEFINED REPORTS, puis sur le bouton Population dynamics dans la fenêtre GRAPHS, puis sur le bouton Seasonal growth dans la fenêtre POPULATION DYNAMICS.

Références

Appeldoorn, R. 1987. Modifications of a seasonal growth function for use with mark-recapture data. J. Cons CIEM 43 : 194-198.

Bertalanffy, L. von et I. Müller. 1943. Untersuchungen über die Gesetzlichkeit des Wachstums. VIII. Die Abhängigkeit des Stoffwechsels von der Korpergrösse und der Zusammenhang von Stoffwechseltypen und Wachstumstypen. Rev. Biol. 35 : 48-95.

Beverton, R.J.H. et S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.

Cloern, J.E. et F.H. Nichols. 1978. A von Bertalanffy growth model with a seasonally varying coefficient. J. Fish. Res. Board Can. 35 : 1479-1482.

Daget, J. et J.M. Ecoutin. 1976. Modéles mathématiques de production applicables aux poissons tropicaux subissant un arrêt annuel prolongé de croissance. Cah. ORSTOM, sér. Hydrobiol. 10(2) : 59-69.

Fulton, T.W. 1901. The rate of growth of the cod, haddock, whiting and Norway pout. 19th Ann. Rep. Fish. Board Scotland. Part III : 154-228.

Fulton, T.W. 1904. The rate of growth of fishes. 22nd Ann. Rep. Fish. Board Scotland. Part III : 141-240.

Longhurst, A. et D. Pauly. 1987. Ecology of tropical oceans. Academic Press, San Diego, California. 407  p.

Pauly, D. 1990. Length-converted catch curves and the seasonal growth of fishes. Fishbyte 8(3) : 33-38.

Pauly, D. 1994. Length-converted catch curves and the seasonal growth of fishes. Fishbyte 8(3) : 24-29.

Pauly, D. et G. Gaschütz. 1979. A simple method for fitting oscillating length growth data, with a program for pocket calculators. I.C.E.S. CM 1979/6 : 24. Demersal Fish Committee, 26 p.

Pauly, D. et J. Ingles. 1981. Aspects of the growth and natural mortality of exploited coral reef fishes, p. 89-98. In E.D. Gomez, C.E. Birkeland, R.W. Buddemeyer, R.E. Johannes, J.A. Marsh et R.T. Tsuda (éds.). Proceedings of the Fourth International Coral Reef Symposium. Vol. 1, Marine Science Center, University of the Philippines, Quezon City.

Pauly, D., M. Soriano-Bartz, J. Moreau et A. Jarre. 1992. A new model accounting for seasonal cessation of growth in fishes. Aust. J. Mar. Freshw. Res. 43 : 1151-1156.

Pitcher, T.J. et P.D.M. MacDonald. 1973. Two models for seasonal growth in fishes. J. Appl. Ecol. 10 : 599-606.

Somer, I.F. 1988. On a seasonally oscillating growth function. Fishbyte 6(1) : 8-11.

Soriano, M. et D. Pauly. 1989. A method for estimating the parameters of a seasonally oscillating growth curve from growth increments data. Fishbyte 7(1) : 18-21.

Ursin, E. 1963a. On the incorporation of temperature in the von Bertalanffy growth equation. Medd. Danm. Fisk. Havunders. N.S. 4(1) : 1-16.

Ursin, E. 1963b. On the seasonal variation of growth rate and growth parameters in Norway pout (Gadus esmarki) in Skagerrak. Medd. Danm. Fisk. Havunders. N.S. 4(2) : 17-29.

Went, A.E.J. 1972. Seventy years agrowing : a history of the International Council for the Exploration of the Sea, 1902-1972. Rapp. P.-v Réun. CIEM 165. 252 p.

Daniel Pauly

Mortalité naturelle

En halieutique, les mortalités sont généralement exprimées sous forme de taux instantanés, c'est-à-dire :

…1)

où et sont les effectifs consécutifs d'une population affectée par un taux (total) de mortalité Z pendant un intervalle de temps .

Cela permet de définir

Z = F + M ...2)

où F est la mortalité par pêche et M la mortalité naturelle, causée par tout facteur autre que la pêche (dans un stock inexploité, Z = M bien évidemment).

 Les estimations de la mortalité naturelle sont généralement difficiles à obtenir (à l'exception des populations non-exploitées, qui ont cependant tendance à être difficiles d'accès pour des études et à devenir de plus en plus rares). Aussi pratiquement toutes les estimations de M bien documentées dans la littérature ont-elles été incorporées dans la table POPGROWTH, qui contient maintenant plus de 400 estimations de mortalité naturelle pour plus de 200 espèces (voir Encadré 17). Environ 42 % de ces enregistrements ont été extraits de Pauly (1980 ; voir également les ‹ Analyses de rendement par recrue ›, ce volume), et 21 % de Beverton et Holt (1959) et Djabali et al. (1993).

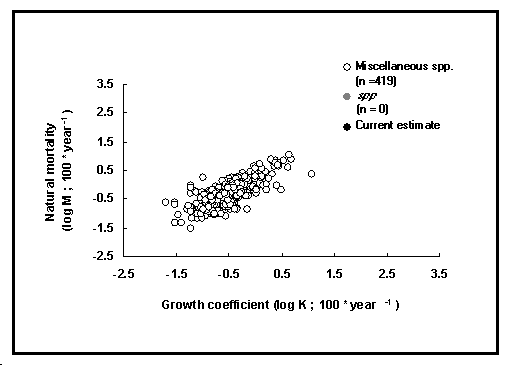
Fig. 23. Mortalité naturelle en fonction du coefficient de croissance pour différents poissons. Voir l’Encadré 17 pour des détails.

Noter que ces valeurs sont toutes indépendantes, c'est-à-dire qu'elles ne sont pas évaluées en utilisant des méthodes ou des modèles empiriques reliant des valeurs de M avec quelque(s) variable(s) prédictrice(s), comme dans Pauly (1980). Ainsi, les estimations de M présentées ici peuvent être utilisées pour définir de nouveaux modèles empiriques.

Étant donné l'importance de ce paramètre, il a paru utile de fournir une estimation de température environnementale moyenne (en °C) pour chaque enregistrement de la table POPGROWTH qui contient une valeur de M. La méthode utilisée pour estimer M est précisée parmi les choix suivants : courbe de captures dans un stock inexploité ; longueur moyenne pour un stock inexploité ; marquage et recapture ; courbe de Z en fonction de l'effort de pêche ; courbe parabolique de Z en fonction des captures ; modèle Ecopath (Christensen et Pauly 1993) ; autre méthode.

Ces techniques sont décrites dans les manuels cités en référence dans ‹ La table POPGROWTH › (ce volume), sauf le modèle Ecopath, brièvement décrit dans l’Encadré 19.

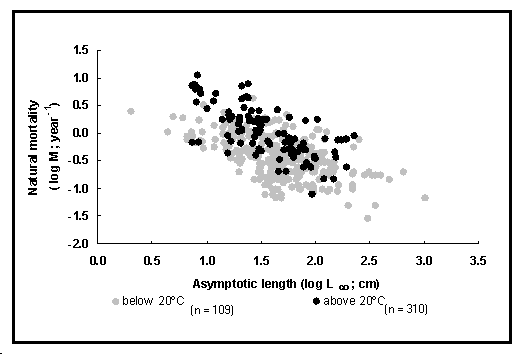
Fig. 24. Mortalité naturelle en fonction de la longueur asymptotique pour les poissons tropicaux (cercles pleins) et les autres poissons (cercles ouverts). Noter l'effet de la température.  Voir Encadré 17 pour plus de détails.

Références

Beverton, R.J.H. et S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme et M. O'Connor (éds.). CIBA Foundation Colloquia on Ageing : the lifespan of animals. Vol. 5, J. & A. Churchill Ltd., London.

Christensen, V. et D. Pauly, Éditeurs. 1993. Trophic models of aquatic ecosystems. ICLARM Conf. Proc. 26, 390 p.

Djabali, F., A. Mehailia, M. Koudil et B. Brahmi. 1993. Empirical equations for the estimation of natural mortality in Mediterranean teleosts. Naga, ICLARM Q. 16(1) : 35-37.

Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2) : 175-192.

Daniel Pauly et Crispina Binohlan

Les analyses de rendement par recrue

Une raison majeure qui a poussé les halieutes à étudier la croissance des poissons, et à la décrire par la courbe de von Bertalanffy (CVB), est l'utilisation du modèle de rendement par recrue (Y/R) de Beverton et Holt (1957) pour l'évaluation des stocks, ou d'un de ses variants.

Aussi avons-nous inclus un bouton Y/R à la table POPGROWTH pour optimiser l'utilisation des paramètres de la CVB. Cliquer sur ce bouton permet d'effectuer diverses analyses de rendement par recrue, dépendant des entrées dans la table et des choix de l'utilisateur. Pour des définitions de certains termes utilisées ci-dessous, voir ‹ La table POPGROWTH ›, ‹ Mortalité naturelle › et ‹ La table LENGTH-WEIGHT › (ce volume).

Néanmoins, avant que les options disponibles ne soient présentées, ‹ recrue › et ‹ rendement par recrue › doivent être définis. Bien que la définition puisse varier selon les auteurs et les pêcheries, nous pouvons concevoir les recrues comme de jeunes poissons complètement métamorphosés dont la croissance est suffisamment bien décrite par la CVB, et dont le taux instantané de mortalité naturelle est supposé similaire à celui des adultes. Ces recrues ont un âge moyen tr, une longueur moyenne Lr et un poids moyen Wr. En atteignant l'âge tr, les recrues peuvent être capturées immédiatement, auquel cas l'âge moyen à la première capture tc est égal à l'âge moyen de recrutement (tc = tr). Ou bien, les recrues ne sont capturées qu'à un âge plus avancé (correspondant à des tailles plus grandes, Lc et Wc). Dans ce cas, à cause de la mortalité naturelle, le nombre de recrues qui entrent réellement dans la pêcherie Rc sera inférieur au nombre initial de recrues Rr, soit

…1)

Pour chaque combinaison de valeurs de tc et F (mortalité par pêche), le rendement par recrue (Y/R = capture en poids, par recrue) peut être estimé en appliquant diverses équations dont la formule exacte dépend principalement du modèle utilisé pour décrire la croissance. Dans les paragraphes suivants, trois formes de la CVB sont données et intégrées aux équations de Y/R.

Cas I : …2)

• qui est la CVB standard (Beverton et Holt 1957), utilisant un ratio isométrique de conversion longueur-poids

  

…3)

où f.c. est le facteur de condition.

Cas II : …4)

• qui est une forme dérivée de la CVB (Pauly 1984) où l'exposant (b) de la relation longueur-poids peut prendre des valeurs différentes de 3, soit

  

…5)

où b 3.

Cas III : …6)

pour la croissance en longueur, et qui peut être utilisée pour des analyses relatives du rendement par recrue quand une relation longueur-poids n'est pas disponible.

L'estimation du rendement par recrue

Cas I :

C'est le modèle original de Beverton et Holt (1957) qui s'exprime :

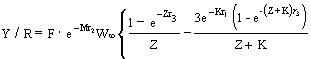
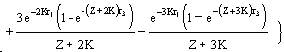…7)

où Z = F + M ;

r1 = tc - t0 ;

r2 = tc - tr ;

r3 = tmax - tc ; et

où W, K et t0 sont des paramètres de croissance (voir ‹ La table POPGROWTH ›, ce volume), tc et tr sont tels que définis ci-dessus, et tmax est l'âge maximal de contribution significative à la pêcherie (Ricker 1980) ou plus simplement, la longévité de l'espèce en question dans les eaux libres (comme contenu dans la table SPECIES). La valeur exacte de tmax a généralement peu d'effet, et ainsi, quand une valeur de tmax n'est pas disponible, l'équation (7) peut être considérablement simplifiée en mettant tmax =  et devient :

…8)

dont les paramètres sont définis comme pour l'équation (7).

Les deux équations (7) et (8) peuvent être utilisées pour évaluer, sur le rendement par recrue, l'effet de valeurs différentes soit de tc et des valeurs de Lc correspondantes, qui peuvent résulter par exemple de l'utilisation de diverses tailles de maille, soit de F, correspondant à divers niveaux d'effort de pêche.

La routine graphique qui est incluse permet de visualiser et d'imprimer deux types de graphiques : (a) des courbes de Y/R (toujours en gan-1) en fonction de F (an-1), pour des valeurs de Lc fixées par l'utilisateur (Fig. 25), ou (b) des diagrammes complets d'isoplèthes (courbes d'égal rendement), qui correspondent à des rendements par recrue pour des valeurs de Lc/L comprises entre 5 et 95 %, et des valeurs de F comprises entre 0 et une limite supérieure (par défaut 5 an-1 ; max. = 20 an-1) fixée par l'utilisateur (voir Fig. 26 et Encadré 18).

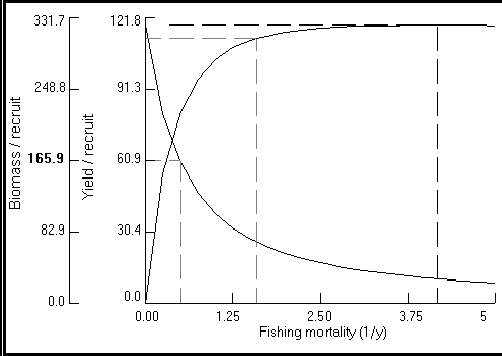
Fig. 25. Courbe bi-dimensionnelle du rendement par recrue pour Plectropomus leopardus. Les paramètres utilisés sont : W = 2 220 g ; K = 0,43 an-1 ; to = 0,34 an ; M = 0,86 an-1 ; b = 3,2 ; tr = 0,12 an ; et tmax = 26 ans. Lc a été estimée à 20 cm. Les courbes descendantes montrent le déclin de la biomasse par recrue (B/R) avec l'augmentation de la mortalité par pêche (F). La courbe ascendante illustre la petite augmentation de rendement quand F est augmenté au-delà de F0.1 = 1,75 an-1. Les unités sont en g pour B/R et en g·an-1 pour Y/R. Les lignes en pointillé indiquent (de gauche à droite) : des valeurs de F où B/R est égal à 50 % de sa valeur initiale (c'est-à-dire, F0.5 ; F0.1) ; et Fmax, tel que défini dans l'Encadré 18.

Fig. 26. Courbe d'isorendement tri-dimensionnelle pour Plectropomus leopardus en fonction de la taille relative à l'entrée dans la pêcherie (Lc/L) et de la mortalité par pêche (F). Les paramètres utilisés sont : L = 45 cm ; M/K = 2 ; tc = 0,12 an ; tmax = 26 ans ; et Lc = 20 cm. Noter la petite variation de Lc/L 0,6 pour le Y/R maximal et F › 1,5 an-1. Voir Encadré 18 pour plus de détails.

Dans toutes ces analyses, M est soit extrait de la table POPGROWTH (voir ‹ Mortalité naturelle ›, ce volume), soit entré par l'utilisateur, soit produit par les équations empiriques de Pauly (1980) qui prennent la forme, pour la longueur :

logM = -0,066 – 0,279logL + 0,6543 logK + 0,4634 logT …9)

et pour le poids :

logM = -0,2107 – 0,0824 logW + 0,6757 logK + 0,4627 logT 10)

où M et K sont exprimés sur une base annuelle, L et W sont respectivement exprimés en cm (LT) et en g (poids vivant), et où T est la température environnementale moyenne (eau) en C. [Une routine interne transforme les valeurs de T pour les basses températures (jusqu'à -2C) en leur équivalents - plus élevés - physiologiquement efficaces (Pauly 1980) ; une autre routine transforme des valeurs de Linitialement exprimées en LS ou LF, en LT, pour les utiliser dans l'équation (9) ; les valeurs pour autres types de mesure (WD, OT ou NA) restent inchangés.]

Les paramètres W et K sont toujours extraits de la table POPGROWTH ainsi que t0 quand il est disponible. D'autre part, une procédure de saisie permet de saisir des valeurs de Lr et de t0 supérieures à 0, leur valeur par défaut (voir Encadré 18) ; noter que Lr doit rester inférieure ou égale à la moitié de L.

Cas II :

L'utilisation des équations (7) et (8) ci-dessus supposent que la croissance en poids est isométrique (c'est-à-dire b = 3). Cette hypothèse n'est pas souvent vérifiée dans la réalité et la valeur de b dans les relations longueur-poids varie généralement entre 2,5 et 3,5 (voir ‹ La table LENGTH-WEIGHT ›, ce volume). L'usage de la fonction incomplète est une méthode qui permet de traiter les valeurs de b 3 (Jones 1957 ; voir aussi Ricker 1975).

Ici, le rendement par recrue, quand tmax = , est donné par

…11)

où X = ;

P = Z/K ;

Q = b + 1 ;

= est le symbole de la fonction beta incomplète, et

r1 et r2 sont définis comme dans l'équation (7).

La procédure Y/R de FishBase vérifie automatiquement si b = 3. Si b 3, l'équation (11) est utilisée (voir Encadré 18). Les valeurs des paramètres utilisées et les affichages sont les mêmes que pour l'équation (8).

Cas III :

Quand les paramètres d'une relation longueur-poids ne sont pas disponibles, les analyses Y/R peuvent encore être exécutées, en utilisant le concept de rendement par recrue relatif (Y'/R) de Beverton et Holt (1964) défini par

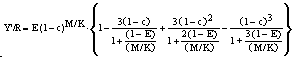…12)

où c = Lc/L, et la proportion de l'exploitation est définie par E = F/Z.

Noter que le rapport entre Y/R et Y'/R est donné, toutes les autres choses étant égales par

…13)

et que le rapport entre F et E est donné par

…14)

Noter aussi que l'échelle E est fortement non linéaire ; pour E = 1, F = . Il s'ensuit que les fortes valeurs de E impliquent des niveaux d'effort trop élevés pour être durables, voire complètement impossible à assurer.

Avertissements concernant l'usage des modèles du rendement par recrue

Les modèles de rendement par recrue, bien qu'élégants et encore adaptés à la gestion de certains stocks, doivent être utilisés avec prudence. Les pêcheurs ne s'intéressent pas à un rendement par recrue imaginaire mais à un rendement physique de poissons qui résulte du rendement par recrue multiplié par le nombre absolu des recrues produites dans le stock. Le rendement est directement proportionnel au rendement par recrue pour une large gamme de mortalité par pêche seulement s’il peut être supposé qu'il n'y a aucun relation, pour une large gamme de F ou de E, entre l'effectif du stock parental et celui de sa progéniture (ce qui n'est pas vrai, voir ‹ La table RECRUITMENT ›, ce volume).

Les valeurs de F ou de E nécessaires pour produire un maximum de rendement par recrue auront ainsi tendance à produire des rendements très bas, parce que Fmax et Emax réduisent généralement le stock parental à un niveau si faible que peu de recrues sont produites. De plus, les résultats des analyses du rendement par recrue ne s'appliquent qu'à long terme ou qu'aux situations d'équilibre. À court terme, une augmentation de mortalité par pêche ou une baisse de la taille à la première capture conduisent toujours à des rendements plus élevés, même quand les analyses de rendement par recrue prédisent des rendements inférieurs. Inversement, une diminution de la mortalité par pêche ou une augmentation de taille à la première capture conduit toujours à des rendements inférieurs à court terme, bien que, à long terme, des rendements plus élevés puissent être atteints. La durée de la période de transition peut être de plusieurs années chez les poissons qui ont une grande longévité et qui sont soumis à une exploitation sur plusieurs années, comme de nombreux stocks tempérés tels que la morue ou le flétan. Chez les poissons de faible longévité, la période de transition sera beaucoup plus courte ; dans le cas de poissons à cycle de vie très court, la distinction entre les effets à court et à long termes ne s'appliquent même pas, parce que les stocks ne sont jamais à l'équilibre.

Une autre caractéristique importante de l'approche du rendement par recrue est que ce rendement par recrue est maximisé à valeurs basses de F ou E seulement dans le cas des grands poissons, de longévité longue. Chez les petits poissons tropicaux à forte valeur de M, les valeurs de F ou E qui maximisent le rendement par recrue sont généralement élevées. Ainsi, gérer une pêcherie tropicale sur une petite espèce (en laissant de côté la pêcherie multi-espèce) en se basant seulement sur des analyses Y/R peut être très trompeur. [Ces considérations ignorent un autre biais dû à l'hypothèse implicite dans les équations (7), (8) et (12) que le recrutement et la sélection des captures se font dans une gamme de taille réduite (recrutement et sélection en lame de couteau) ; voir Pauly et Soriano 1986 ; Silvestre et al. 1991.]

Pour cette raison et quelques autres, il est généralement accepté de limiter F au point où la pente de la courbe du rendement par recrue est égale à 1/10ème de sa valeur à l'origine (Gulland et Boerema 1973). Ce concept, appelé F0,1, peut être envisagé comme un substitut du REM (Rendement Économique Maximal), applicable dans les situations où les données économiques sur la performance d'une pêcherie ne sont pas disponibles. Un concept analogue à F0,1, mais appliqué à E est E0,1, est utilisé dans le Cas III ci-dessus.

Une autre précaution d'utilisation des analyses Y/R est de toujours examiner la courbe correspondante de biomasse par recrue (B/R ou B'/R) calculée avec le rendement par recrue (on obtient B/R en divisant Y/R par F simplement, voir l'équation 8 par exemple). Ici, le point de référence approprié est la valeur de F (ou E) qui réduit B/R (ou B'/R) à la moitié de son niveau non exploité (quand F ou E = 0), c'est-à-dire au niveau de biomasse qui théoriquement maximise la production excédentaire et permet une ‹ production maximum équilibrée › (PME) (voir Schaefer 1954, 1957 ; Gulland 1983 ; ou Pauly 1984). Ce niveau est référencé ici F0,5 ou E0,5 .

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population Dynamics dans la vue BIOLOGY, puis sur le bouton Growth dans la fenêtre POPULATION DYNAMICS et après avoir sélectionné une étude (une ligne), sur le bouton Y/R dans la vue POPULATION GROWTH INFORMATION. Ou bien, vous pouvez passer successivement par les boutons Reports, Graphs, Population dynamics, Y/R Analyses à partir de la fenêtre MAIN MENU.

Références

Beverton, R.J.H. et S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.

Beverton, R.J.H. et S.J. Holt. 1964. Table of yield functions for fishery management. FAO Fish. Tech. Pap. 38, 49 p.

Gulland, J.A. 1983. Fish stock assessment : a manual of basic methods. FAO/Wiley, Chichester, New York. 223 p.

Gulland, J.A. et L. Boerema. 1973. Scientific advice on catch levels. Fish. Bull. (US) 71 : 325-335.

Jones, R.E. 1957. A much simplified version of the fish yield equation. Doc. No. P. 21. Paper presented at the Lisbon joint meeting of International Commission Northwest Atlantic-Fisheries, International Council for the Exploration of the Sea, and Food and Agriculture Organization of the United Nations. 8 p. [Mimeo].

Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2) : 175-192.

Pauly, D. 1984. Fish population dynamics in tropical waters : a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.

Pauly, D. et M. Soriano. 1986. Some practical extensions to Beverton and Holt's relative yield-per-recruit model, p. 491-495. In J.L. Maclean, L.B. Dizon et L.V. Hosillos (éds). The First Asian Fisheries Forum. Asian Fisheries Society, Manila.

Ricker, W.E. 1980. Calculs et interprétation des populations de poissons. Bull. Fish. Res. Board Can. 191F, 409 p.

Schaefer, M.B. 1954. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-Am. Trop. Tuna Comm., Bull. 1(2) : 27-56.

Schaefer, M.B. 1957. A study of the dynamics of the fishery for yellowfin tuna in the eastern tropical Pacific Ocean. Inter-Am. Trop. Tuna Comm., Bull. 2 : 247-268.

Silvestre, G., M. Soriano et D. Pauly. 1991. Sigmoid selection and the Beverton and Holt equation. Asian Fish. Sci. 4(1) : 85-98.

Daniel Pauly et Felimon C. Gayanilo, Jr.

La table RECRUITMENT

Les fluctuations du recrutement et leurs causes représentent une des voies principales de recherche en halieutique, ce qui n'est pas surprenant tant il est vrai que ces variations déterminent les niveaux de captures annuels des pêcheries.

La prévision précise d'un recrutement futur n'est pas possible. Cependant, de grandes généralisations sont possibles (par exemple, que les stocks épuisés produisent moins de recrues que des stocks encore abondants est un résultat qui n'est pas trivial). Plus des séries chronologiques de recrutement seront disponibles de différents points du globe, plus ces généralisations seront précises et fiables.

Aussi nous sommes-nous réjouis quand R.A. Myers a offert d'incorporer dans FishBase la base de données complète de séries chronologiques de recrutement et des informations afférentes que lui et ses prédécesseurs au North West Atlantic Fisheries Center, Science Branch, Department of Fisheries and Oceans, St. John's, Canada, avaient minutieusement rassemblées (Myers et al. 1990, 1995). En attendant un texte plus complet de R.A. Myers (maintenant à la Dalhousie University, Halifax, Nova Scotia, Canada), les paragraphes ci-dessous décrivent brièvement la structure que nous avons créée pour stocker ces données.

En premier lieu, la vue RECRUITMENT indique les stocks dont une série de recrutement (et toute autre série associée) est disponible pour une espèce donnée. Double-cliquer sur un tel stock mène à la vue RECRUITEMENT SERIES.

Les champs

La méthode utilisée pour établir la série chronologique de recrutement (et les séries apparentées) est indiquée parmi les choix suivants :

1. comptages directs ;
2. données de prise/effort ;
3. la pêche électrique ;
4. marquage-recapture ;
5. analyse de population virtuelle (APV) ;
6. reconstruction du stock ;
7. campagne de recherche ; et
8. voir les informations supplémentaires.

De plus, sont indiqués le groupe d'âge utilisé pour estimer la mortalité par pêche, le décalage de recrutement, c'est-à-dire l'âge au recrutement (tr en années), et la localité, avec la latitude et la longitude du mi-point central de la répartition du stock. Enfin, les autres composants de la base de données fournie par R.A. Myers qui n'ont pas pu être assignés aux quelques champs existants sont regroupés dans un champ mémo.

Les dénombrements des séries chronologiques de recrutement et les estimations correspondantes des quantités débarquées, de la biomasse du stock reproducteur et/ou de la mortalité par pêche sont affichées en cliquant sur les boutons ‹ graphique › ou ‹ tableau ›. Noter cependant que, dans les graphiques, les séries sont exprimées en unités relatives (rapportées à la valeur maximale) (voir le Fig. 27). Cliquer sur le bouton ‹ tableau › pour afficher les données brutes.

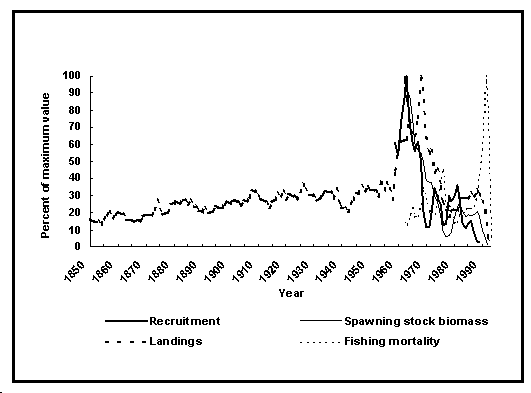
Fig. 27. Série chronologique des quantités débarquées, de la biomasse du stock reproducteur, du recrutement et de la mortalité par pêche de la morue atlantique (Gadus morhua) autour de Terre-Neuve, Canada. Noter comment le développement des pêcheries modernes, au début des années 1960, a détruit une pêcherie qui avait été équilibrée (durable) pendant les 4 derniers siècles.

Un graphique permet d'apprécier la variabilité globale des séries disponibles. Un autre graphique (voir Fig. 28) illustre le rapport entre la taille du stock parental et le recrutement subséquent.

Plus de 600 séries sont maintenant disponibles pour environ 120 espèces. Tout utilisateur qui souhaiterait contribuer à cette table devrait contacter R.A. Myers, qui continuera à en assurer la mise à jour (Myers@phys.ocean.dal.ca).

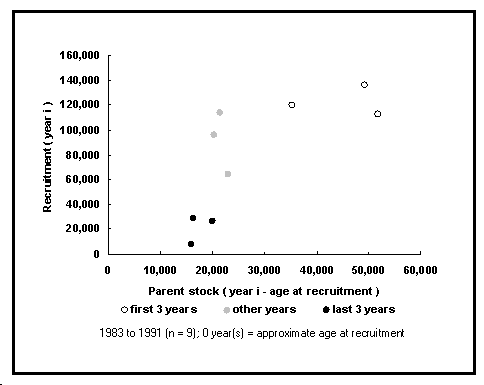
Fig. 28. Exemple d'un rapport entre recrutement et stock parental : Merluccius merluccius dans la zone ICES VIIIc et IXa. Noter les symboles utilisés pour identifier le début et la fin d'une série.

Comment y arriver

Cliquer sur le bouton Biology dans la vue SPECIES, puis sur le bouton Population Dynamics dans la vue BIOLOGY, puis sur le bouton Recruitment dans la fenêtre POPULATION DYNAMICS.

Remerciements

Nous remercions R.A. Myers et ses collègues pour avoir confié leur précieuse base de données à FishBase.

Références

Myers, R.A., W. Blanchard et K.R. Thompson. 1990. Summary of North Atlantic fish recruitment, 1942-1987. Can. Tech. Rep. Fish. Aquat. Sci. No. 1743.

Myers, R.A., J. Bridson et N.J. Barrowman. 1995. Summary of worldwide stock and recruitment data. Can. Tech. Rep. Fish. Aquat. Sci. No. 2024.

Daniel Pauly et Crispina Binohlan