Length-weight relationships are important in fisheries science, notably to raise length-frequency samples to total catch, or to estimate biomass from underwater length observations. The LENGTH-WEIGHT table presents the a and b values of over 5,000 length-weight relationships of the form W = a × Lb, pertaining to about over 2,000 fish species.
The units of length and weight in FishBase are centimeter and gram, respectively. Thus when length-weight relationships are not in cm-g, the intercept 'a' is transformed as follows:
a'(cm, g) = a (mm, g)*10^b
However, published length-weight relationships are sometimes difficult to use, as they may be based on a length measurement type (e.g., fork length) different from one’s length measurements (expressed e.g., as total length).
Therefore, to facilitate conversion between length types, an additional LENGTH-LENGTH table, presented below, was devised which presents linear regressions or ratios linking length types (e.g., FL vs. TL).
a'(cm, g) = a (cm, kg)*1000
a'(cm, g) = a (mm, mg)*10^b/1000
a'(cm, g) = a (mm, kg)*10^b*1000
The length-weight relationships themselves were derived from over 1,000 references, e.g., Carlander (1969, 1977); Cinco (1982); Dorel (1985); Bohnsack and Harper (1988); Coull et al. (1989); Torres (1991); and Kulbicki et al. (1993).
We included a calculated field with the weight of a 10 cm fish (which should be in the order of 10 g for ‘normal’, fusiform shaped fish), to allow identification of gross errors, given knowledge of the body form of a species. Also, a graph button in the summary table, when clicked on displays length-weight relationships (Fig. 17). This can be used to identify curves that deviate from the general trend.
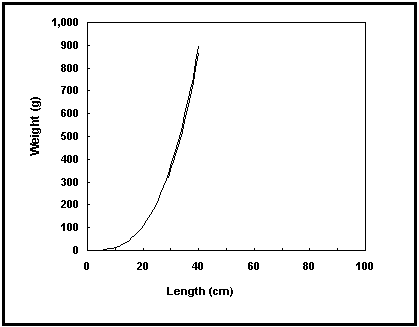
Fig. 17. The two length-weight relationships presently available in FishBase for Lutjanus
bohar. Note that you can use the graph to estimate weight at a given length.
A choice field indicating the method used to estimate the parameters a and b of length-weight relationships has been added to this table. These methods are:
Type I (or ‘predictive’) linear regression of logW vs. logL (the method of choice in the overwhelming majority of cases);
Type II (or ‘functional’) linear regression of logW vs. logL (as suggested by Ricker 1975, but rarely used, given that length-weight relationships are generally used to predict W from L);
Same as (1) or (2), but with correction for bias suggested by Sprugel (1983; see also Vakily et al. 1986);
Nonlinear regression of W vs. L, as recommended e.g., by Saila et al. (1988);
From length-frequency samples and their bulk weights, using the algorithm of Pauly and Gayanilo (1996);
By setting b = 3, and using a single pair of L-W values to calculate a;
By setting b = 3, and using the geometric mean of L and W values to solve for ‘a’, or by calculating ‘a’ for each data pair, then taking the mean of the resulting values of ‘a’;
Any other method (e.g., that of Lenarz 1994; to be specified in the Comment field).
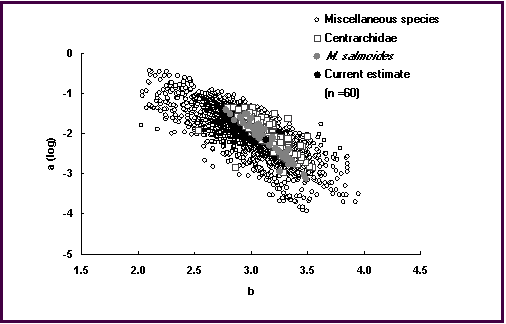
Fig. 18. Plot of length-weight relationships (log a vs. b) available for Micropterus salmoides. Note questionable dot
at a (log) »
- 3 and b »
3.25, which falls below the line formed by the other estimates for the species. Users can enter and plot their own estimate for comparisons.
Evaluating the quality of length-weight relationships is not easily done, as there are only ‘rules of thumb’ for what the values of ‘a’ and ‘b’ should be. For example, one would expect a » 0.001 for eel-like fishes and b > 3 for fishes that increase more in weight than predicted by their increase in length, such as in many morays. While exploring such relationships, we discovered that a plot of log a over b forms a straight line for most species with several length-weight relationships available, such as in Micropterus salmoides (Fig. 18). Estimates that are clearly below or above that line appear to be questionable. We have added an option to that graph where users can enter their estimates of ‘a’ and ‘b’ for the respective species and see how it compares against all other estimates. The graph is also available on the Internet version. We are currently exploring other ramifications of this graph, such as the factors determining the length and the slope of the line formed by the specific dots.
Rainer Froese
You get to the LENGTH-WEIGHT table by clicking on the Biology button in the SPECIES window, the Population dynamics button in the BIOLOGY window and the L-W relationship button in the POPULATION DYNAMICS window. The internal name of this table is POPLW table.
On the Internet, you access this table by clicking on the L-W relationship link in the ‘More information’ section of the ‘Species Summary’ page. Alternatively, you can click on the L-W relation radio button in the ‘Information by Topic’ section of the ‘Search FishBase’ page.
Bohnsack, J.A. and D.E. Harper. 1988. Length-weight relationships of selected marine reef fishes from the southeastern United States and the Caribbean. NOAA Tech. Mem. NMFS-SEFC-215, 31 p.
Carlander, K.D. 1969. Handbook of freshwater fishery biology. Vol. 1. The Iowa State University Press, Ames, Iowa. 752 p.
Carlander, K.D. 1977. Handbook of freshwater fishery biology. Vol. 2. The Iowa State University Press, Ames, Iowa. 431 p.
Cinco, E. 1982. Length-weight relationships of fishes, p. 34-37. In D. Pauly and A.N. Mines (eds.) Small-scale fisheries of San Miguel Bay: biology and stock assessment. ICLARM Tech. Rep. 7, 124 p.
Coull, K.A., A.S. Jermyn, A.W. Newton, G.I. Henderson and W.B. Hall. 1989. Length-weight relationships for 88 species of fish encountered in the North Atlantic. Scottish Fish. Res. Rep. 43, 80 p.
Dorel, D. 1985. Poissons de l'Atlantique nord-est: relations taille-poids. Institut Français de Recherche pour l'Exploration de la Mer, Paris. 165 p.
Kulbicki, M., G. Mou Tham, P. Thollot and L. Wantiez. 1993. Length-weight relationships of fish from the lagoon of New Caledonia. Naga, ICLARM Q. 16(2-3):26-29.
Lenarz, W.H. 1994. Estimation of weight-length relationship from group measurements. US Fish. Bull. 93:198-202.
Pauly, D. and F.C. Gayanilo, Jr. 1996. Estimating the parameter of length-weight relationship from length-frequency samples and bulk weights, p. 136. In D. Pauly and P. Martosubroto (eds.) Baseline studies of biodiversity: the fish resources of western Indonesia. ICLARM Stud. Rev. 23, 321 p.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. B. Can. 191, 382 p.
Saila, S.B., C.W. Recksiek and M.H. Prager. 1988. Basic fishery science programs: a compendium of microcomputer programs and manual of operation. Elsevier Science Publishing Co., New York. 230 p.
Sprugel, D.G. 1983. Correcting for bias in log-transformed allometric equations. Ecology 64(1):209-210.
Stergiou, K.I. and D.K. Moutopoulos. 2001. A review of length-weight relationships of fishes from Greek marine waters. Naga ICLARM Q. 24(1&2):23-39.
Torres, F. Jr. 1991. Tabular data on marine fishes from Southern Africa, Part I. Length-weight relationships. Fishbyte 9(1):50-53.
Vakily, J.M., M.L. Palomares and D. Pauly. 1986. Computer programs for fish stock assessment: applications for the HP41 CV calculator. FAO Fish. Tech. Pap. 101 Suppl. 1, 255 p. Rome.