viz.:
![]() …1)
…1)
where ![]()
![]() are successive numbers in a population, affected by a (total) mortality rate Z during a time interval
are successive numbers in a population, affected by a (total) mortality rate Z during a time interval ![]() .
.
This allows defining
Z = F + M ...2)
where F is the fishing mortality and M is the natural mortality, caused by any factor other than fishing (in an unexploited stock, we obviously have Z = M).
Natural mortality estimates are usually hard to obtain (except in unfished populations, which tend to be inaccessible for study and are becoming scarcer). Thus, every well-documented estimate of M so far encountered in the literature has been incorporated in the POPGROWTH table, which now includes over 400 estimates of natural mortality, for over 200 species (see Box 19). About 42% of these are from Pauly (1980; see also Yield-per-recruit Analyses) while 20% are from Beverton and Holt (1959) and Djabali et al. (1993).
The FishBase graphs of natural mortality are based on what is surely the largest compilation of independently derived natural mortality estimates of fish in the world, i.e., similar, but independent data do not exist which could be used to verify the generalizations derived from this dataset. Thus, since independent replication of our results is difficult, we must be very careful in presenting generalizations based on this dataset.
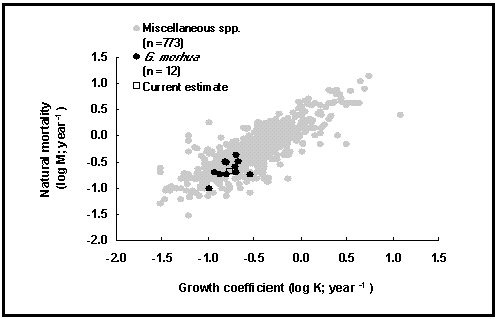
Here, we have therefore limited ourselves to two graphs testing earlier generalizations of Beverton and Holt (1959) and Pauly (1980). The first of these graphs (Fig. 27) is a plot of logM vs. logK, the curvature parameters of the von Bertalanffy growth function. As might be seen, this confirms that K, which is related to longevity, is a good predictor of M. The variance is high, however, suggesting that other factors also influence M.
Our second graph (Fig. 28) documents two of the factors influencing M, size and environmental temperature. The dots are estimates of logM vs. the corresponding estimates of logL¥
, with open dots for estimates from waters below 20°
C (about 2/3 of all cases), and full dots for the rest, referring to tropical fishes.
As might be seen, M is not only related to L¥
(and to K; see Fig. 27), but also to temperature, notwithstanding Charnov (1993), whose concepts of ‘Beverton and Holt invariants’, of which M/K is supposed to be one, do not allow for the temperature effect so evident in the data at hand.
References
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O’Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol 5, J. & A. Churchill Ltd., London.
Charnov, E. 1993. Life-history invariants: some explorations of symmetry in evolutionary ecology. Ecology and Evolution. Oxford University Press, Oxford. 128 p.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly
Note that except in a few cases explicitly listed as such, these estimates are independent, i.e., were not estimated using rules of thumbs, or empirical models linking values of M with some predictor variable(s), as presented by Pauly (1980) or Hoenig (1984). Thus, the estimates of M presented here may be used to derive new empirical models (Froese et al. in prep.).
Hoenig’s (1984) model takes:
ln = 1.44 – 0.984 ln(tmax)
where tmax is the longevity of the fish in question, in years×
Combined with the highest tmax values on record (in the SPECIES table), this yields approximate values of M in species for which there is little hope that more precise estimates will ever become available. These values (and a few other, non-independent estimates of M) are identifiable as such by the method used (see below).
Fig. 27. Natural mortality vs. growth coefficient for various fishes. See Box 19 for details.
An estimate of mean environmental temperature (in °C) was added to every POPGROWTH record that included an estimate of M. Also, the method used to estimate M is recorded, using one of the following choices: length-converted catch curve in unexploited population; age-structured catch curve in unexploited population; mean length in unexploited population; tagging-recapture data; plot of Z on effort; parabolic plot of Z on catch; Ecopath (trophic) model (Christensen and Pauly 1993); from tmax and Hoenig’s model; other non-independent estimate; and other method. In the last two cases, a comment is provided in the Remarks field.
These methods are described in the textbooks cited in the POPGROWTH table, except for that involving the Ecopath model, briefly described in Box 21.
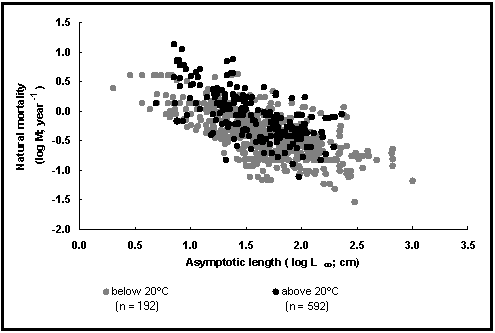
Fig. 28. Natural mortality vs. asymptotic length for tropical fishes and other fishes. Note temperature effect, and
see Box 19 for details.
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O’Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol. 5, J. & A. Churchill Ltd., London.
Christensen, V. and D. Pauly, Editors. 1993. Trophic models of aquatic ecosystems. ICLARM Conf. Proc. 26, 390 p.
Djabali, F., A. Mehailia, M. Koudil and B. Brahmi. 1993. Empirical equations for the estimation of natural mortality in Mediterranean teleosts. Naga, ICLARM Q. 16(1):35-37.
Froese, R., C. Binohlan and D. Pauly. Empirical equations to estimate natural mortality in fishes. (In prep.).
Hoenig, J. 1984. Empirical use of longevity data to estimate mortality rates. Fish. Bull. (US) 81(4): 898-903.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly and Crispina Binohlan