Una razón importante por la que los científicos pesqueros estudian el crecimiento de los peces, y lo describen con la curva de von Bertalanffy (CVB), es para poder hacer la evaluación de los stocks mediante el uso del modelo de rendimiento por recluta (Y/R) de Beverton y Holt (1957), o alguna de sus variantes.
También hemos incluido un botón Y/R en la tabla POPGROWTH para optimizar el uso de los parámetros de la CVB. Haga clic sobre este botón para efectuar diversos análisis de rendimiento por recluta, dependiendo de las entradas de la tabla, y de las opciones escogidas por el usuario. Para las definiciones de ciertos términos usados más abajo, véase ‹ La tabla POPGROWTH ›, ‹ Mortalidad natural › y ‹ La tabla LENGTH-WEIGHT › (este volumen).
De todas maneras, antes de presentar las opciones disponibles, ‹ recluta › y ‹ rendimiento por recluta › deben ser definidos. Aunque la definición pueda variar según los autores y las pesquerías, nosotros entendemos el término recluta como los peces juveniles completamente metamorfoseados cuyo crecimiento está bien descrito por la CVB, y cuya tasa instantánea de mortalidad natural se supone similar a la de los adultos. Estos reclutas tienen una edad media tr, una longitud media Lr y un peso medio Wr. Al llegar a la edad tr, los reclutas pueden ser capturados inmediatamente, y en ese caso la edad media de la primera captura tc es igual a la edad media de reclutamiento (tc = tr). O bien, los reclutas no son capturados hasta una edad más avanzada (correspondiente a tallas mayores, Lc y Wc). En este caso, a causa de la mortalidad natural, el número de reclutas que entran realmente en la pesquería Rc será inferior al número inicial de reclutas Rr, es decir
![]()
![]() …1)
…1)
Para cada combinación de valores de tc y F (mortalidad por pesquería), el rendimiento por recluta (Y/R = captura en peso, por recluta) puede ser estimado aplicando diversas ecuaciones cuya formula exacta depende principalmente del modelo usado para describir el crecimiento. En los párrafos siguientes, se proporcionan tres formas de la CVB integradas a las ecuaciones de la estima de Y/R.
Caso I: ![]() …2)
…2)
que es la CVB estándar (Beverton y Holt 1957), usando una proporción isométrica de conversión talla-peso
![]() …3)
…3)
donde f.c. es el factor de condición.
Caso II: ![]() …4)
…4)
que es una forma derivada de la CVB (Pauly 1984) donde el exponente (b) de la relación talla-peso puede tomar valores distintos de 3, es decir
![]() …5)
…5)
donde b ¹ 3.
Caso III: ![]() …6)
…6)
para el crecimiento en longitud, y que puede ser usada para los análisis relativos del rendimiento por recluta cuando una relación talla-peso no está disponible.
La estima del rendimiento por recluta
Caso I Es el modelo original de Beverton y Holt (1957) que se expresa:
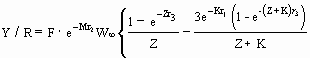
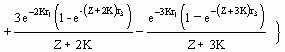 …7)
…7)
donde Z = F + M ;
r1 = tc - t0 ;
r2 = tc - tr ;
r3 = tmax - tc ; y
donde W¥, K y t0 son los parámetros de crecimiento (véase ‹ La tabla POPGROWTH ›, este volumen), tc y tr están definidos más arriba, y tmax es la edad maxima de contribución significativa a la pesquería (Ricker 1980) o más simplemente, la longevidad de la especie en cuestión en las aguas libres (proporcionada en la tabla SPECIES). El valor exacto de tmax tiene generalmente poco efecto, y de esta manera, cuando un valor de tmax no está disponible, la ecuación (7) puede ser considerablemente simplificada ajustando tmax = ¥ de lo cual aparece:
![]() …8)
…8)
cuyos parámetros son definidos como para la ecuación (7).
Las dos ecuaciones (7) y (8) pueden ser usadas para evaluar, sobre el rendimiento por recluta, el efecto de valores diferentes ya sea de tc y de los valores de Lc correspondientes, que pueden resultar por ejemplo del uso de diversos anchos de malla, o bien de F, correspondiente a diversos niveles de esfuerzo de pesquería.
La rutina gráfica incluida permite visualizar e imprimir dos tipos de gráficos : (a) las curvas de Y/R (siempre en g×año?1) en función de F (año?1), para los valores de Lc fijados por el usuario (Fig. 25), o (b) los diagramas completos de isopletas (curvas de igual rendimiento), que corresponden a los rendimientos por recluta para los valores de L,sub>c/L¥ comprendidos entre 5 y 95%, y los valores de F comprendidos entre 0 y un límite superior (por defecto 5 año?1 ; max. = 20 año?1) fijado por el usuario (véase Fig. 26, y Recuadro 18).
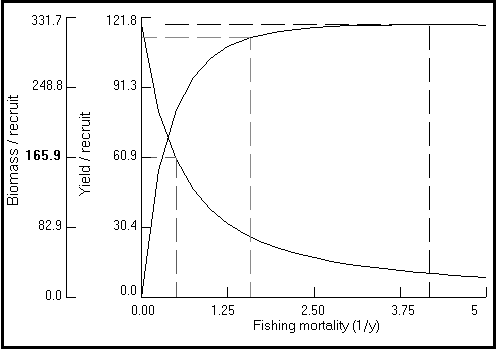
Fig. 25. Curva bidimensional del rendimiento por recluta para Plectropomus leopardus. Los parámetros usados son : W¥ = 2 220 g ; K = 0,43 año?1 ; to = 0,34 año ; M = 0,86 año?1 ; b = 3,2 ; tr = 0,12 años ; y tmax = 26 años. Lc fue fijada en 20 cm. Las curvas descendientes muestran el declive de la biomasa por recluta (B/R) con el aumento de la mortalidad por pesquería (F). La curva ascendente ilustra el pequeño aumento de rendimiento cuando F aumenta más allá de F0.1 = 1,75 año?1. Las unidades son en g para B/R y en g·año?1 para Y/R. Las líneas de puntos indican (de izquierda a derecha) : valores de F donde B/R es igual a 50% de su valor inicial (es decir, F0.5 ; F0.1) ; y Fmax, como fue definido en el Recuadro 18.
En todos estos análisis, M se extrae de la tabla POPGROWTH (véase ‹ Mortalidad natural ›, este volumen), o se introduce por el usuario, o se produce por las ecuaciones empíricas de Pauly (1980) que para la longitud toman la forma:
logM = -0.066 - 0.279logL¥ + 0.6543 logK + 0.4634 logT …9)
y para el peso:
logM = -0.2107 - 0.0824 logW¥ + 0.6757 logK + 0.4627 logT 10)
donde M y K son expresados sobre una base anual, L¥ y W¥ son respectivamente expresados en cm (LT) y en g (peso en vivo), y donde T es la temperatura ambiental media (agua) en °C. [Una rutina interna transforma los valores de T para las bajas temperaturas (hasta -2°C) en sus equivalentes - más altas - fisiológicamente eficaces (Pauly 1980) ; otra rutina transforma los valores de L¥ inicialmente expresados en LS o LF, en LT, para utilizarlos en la ecuación (9) ; los valores para otros tipos de medida (WD, OT o NA) no varían.]
Los parámetros W¥ y K se extraen siempre de la tabla POPGROWTH así como t0 cuando está disponible. Por otra parte, una rutina de entrada permite introducir los valores de Lr y de t0 superiores a 0, su valor por defecto (véase Recuadro 18) ; Nótese que Lr debe ser inferior o igual a la mitad de L¥.
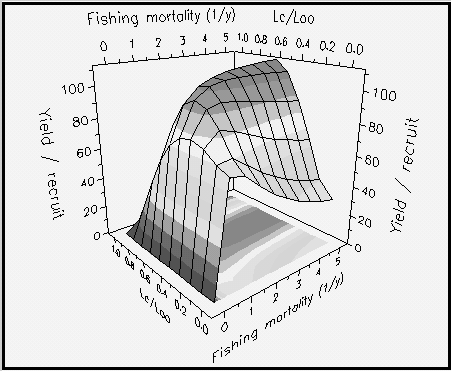
Fig. 26. Curva de iso-rendimiento tridimensional para Plectropomus leopardus en función de la talla relativa a la entrada en la pesquería (Lc/L ¥), y de la mortalidad por pesquería (F). Los parámetros usados son : L ¥ = 45 cm ; M/K = 2 ; tc = 0,12 año ; tmax = 26 años ; y Lc = 20 cm. Nótese la pequeña variación de Lc/L ¥ " 0,6 para Y/R máxima y F › 1,5 año?1. Véase Recuadro 18 para más detalles.
Case II
El uso de las ecuaciones (7) y (8) de más arriba supone que el crecimiento en peso es isométrico (es decir b = 3). Esta hipótesis no está a menudo verificada en la realidad y el valor de b en las relaciones talla-peso varía generalmente entre 2,5 y 3,5 (véase ‹ La tabla LENGTH-WEIGHT ›, este volumen). El uso de la función incompleta b -es un método que permite tratar los valores de b ¹ 3 (Jones 1957 ; véase también Ricker 1975).
Recuadro 18. Los gráficos de rendimiento por recluta y de biomasa por recluta.
La rutina Y/R incluida en FishBase está realizada de manera que las curvas Y/R y B/R sean calculadas incluso si tansolo los valores de L ¥ y K están disponibles en la tabla POPGROWTH. Los valores por defecto son establecidos para los parámetros que faltan de la manera siguiente:
El caso I (véase ‹ Los análisis de rendimiento por recluta ›, este volumen) se usa cuando W¥ está disponible y b = 3. La curva inicial supone que tr = 0, t0 = 0 (salvo si están disponibles en la tabla POPGROWTH), y Lc = 0,05 × L¥. M se trata como en el caso III, pero es la ecuación (10) la que se usa para estimar el valor de M. Los parámetros tr y t0 pueden ser cambiados con posterioridad : tr entrando un valor de Lr (una rutina interna la transforma en tr) ; t0 entrando un valor por elección, o según una evaluación aproximada calculada a partir de la ecuación empírica siguiente:
log(-t0) »
-0.3922 - 0.2752 logL¥
- 1.038 logK
donde L¥está en cm (LT), y K en año?1. Ésta se basa en 153 tripletes de valores de t0, L¥ y K seleccionados por Pauly (1978) para tratar una amplia diversidad taxonómica y de talla (Pauly 1979). Si se dispone de un valor de tmax en la tabla SPECIES, la ecuación (7) permite tenerlo en cuenta; alternativamente, la ecuación (8) se usa con tmax = ¥.
El caso II se usa cuando W¥ está disponible y b ¹ 3 ; t0, tr, Lc y M son tratados como en el caso I.
El caso III se usa cuando no disponemos de W¥,, en cuyo caso debe usarse L¥,. Se asume que b = 3, t0 = 0, tmax = ¥,, tr = 0, y Lc = 0,05 × L¥,. Se proporcionan rutinas para la introducción de valores de M diferentes del proporcionado por defecto, fijado en M = 2K (una de las rutinas usa la ecuación (9) que requiere la entrada de un valor de T en °C), y para variar el valor de Lc.
Las curvas de biomasa presentadas con los análisis Y/R son calculadas a partir de versiones modificadas de las ecuaciones (7), (8), y (12), y deberían ser tenidas en cuenta para la interpretación de las curvas de Y/R (véase más abajo).
Las curvas se muestran de dos formas: (1) en dos dimensiones, con las curvas de Y/R y B/R en función de Lc; y (2) en tres dimensiones en forma de diagramas de isopletas (rendimiento o biomasa). Las curvas en dos dimensiones presentan tres puntos de referencia:
Emax o Fmax, el valor de E o de F para el valor máximo de Y/R posible para un valor determinado de Lc;
E0,1 y F0,1, el valor de E o de F donde la pendiente de Y/R es igual a 1/10 de su valor en el origen ; y
E0,5 y F0,5, los valores de E o de F asociados con una reducción del 50% de la biomasa por recluta en el stock inexplotado.
Estos puntos de referencia, correspondientes a las tres líneas de puntos verticales de la figura 25, son discutidos en la conclusión de ‹ el análisis de rendimiento por recluta ›, este volumen.
Bibliografía
Pauly, D. 1978. A preliminary compilation of fish length growth performance. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 63, 156 p.
Daniel Pauly
Aquí, el rendimiento por recluta, cuando tmax = ¥, viene dado por
![]() …11)
…11)
where X = ![]() ;
;
P = Z/K ;
Q = b + 1 ;
b
= es el símbolo de la función beta incompleta, y
r1 y r2 se definen como en la ecuación (7).
La rutina Y/R de FishBase verifica de manera automática si b = 3. Si b ¹ 3, se usa la ecuación (11) (véase Recuadro 18). Los valores de los parámetros usados y las muestras son los mismos que para la ecuación (8).
Caso III
Cuando los parámetros de una relación talla-peso no están disponibles, los análisis Y/R todavía pueden ser ejecutados, usando el concepto de rendimiento relativo por recluta (Y'/R) de Beverton y Holt (1964) definido por
donde c = Lc/L¥, y la proporción de la explotación se define por E = F/Z.
Nótese que, siendo todas las otras cosas iguales, la relación entre Y/R e Y'/R se determina por
y que la relación entre F y E se determina por
Nótese también que la escala en E es fuertemente no lineal ; para E=1, F=¥. Así pues, altos valores de E implican niveles de esfuerzo demasiado altos para ser perdurables o incluso para llegar a conseguirse.
Advertencias que conciernen al uso de los modelos de rendimiento por recluta
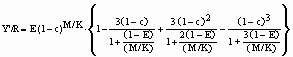 …12)
…12)![]() … 13)
… 13)![]() …14)
…14)
Los modelos de rendimiento por recluta, aunque elegantes y todavía válidos para la gestión de ciertos stocks, deben ser usados con prudencia. Los pesqueros no están interesados en un rendimiento por recluta imaginario sino en un rendimiento físico de peces que resulta del rendimiento por recluta multiplicado por el número absoluto de reclutas producidos en el stock. El rendimiento es directamente proporcional al rendimiento por recluta para una amplia gama de mortalidad por pesquería solamente si se puede asumir que no hay relación, para una amplia gama de F o de E, entre el efectivo del stock parental y el efectivo del reclutamiento (lo cual no es cierto, véase ‹ La tabla RECRUITMENT ›, este volumen).
Los valores de F o de E necesarios para producir un máximo rendimiento por recluta tendrán pues tendencia a producir rendimientos muy bajos, porque Fmax y Emax reducen generalmente el stock parental a un nivel tan débil que pocos reclutas son producidos. Además, los resultados de los análisis del rendimiento por recluta no se aplican más que a largo plazo o en situaciones de equilibrio. A corto plazo, un incremento de mortalidad por pesquería o un decremento de la talla en la primera captura conducen siempre a rendimientos más elevados, incluso cuando los análisis de rendimiento por recluta predicen rendimientos inferiores. A la inversa, un decremento de la mortalidad por pesquería o un incremento de la talla en la primera captura conducen siempre a rendimientos inferiores a corto plazo, aunque a largo plazo puedan alcanzarse rendimientos más altos. La duración del periodo de transición puede ser de muchos años en los peces que tienen una longevidad elevada y que están sometidos a una explotación de muchos años, como numerosos stocks de aguas templadas como el bacalao o el fletán. En los peces de menor longevidad, el periodo de transición será mucho más corto ; en el caso de peces de ciclo vital muy corto, la distinción entre los efectos a corto y a largo plazo ni se aplican, porque los stocks no están nunca en equilibrio.
Otra característica importante del enfoque del rendimiento por recluta es que este rendimiento por recluta está maximizado para valores bajos de F o E solamente en el caso de los grandes peces, de longevidad importante. En los pequeños peces tropicales con valores de M elevados, los valores de F o E que maximizan el rendimiento por recluta son generalmente altos. De esta manera, gestionar una pesquería tropical sobre una especie pequeña (dejando de lado la pesquería multi-específica) basándose solamente en los análisis Y/R puede ser muy engañoso. [Estas consideraciones ignoran otro sesgo debido a la hipótesis implícita en las ecuaciones (7), (8) y (12) que el reclutamiento y la selección de las capturas se hacen en una gama de talla reducida (reclutamiento y selección 'al filo de la navaja' (knife-edge recruitment and selection)) ; véase Pauly y Soriano 1986 ; Silvestre et al. 1991.]
Por esta y algunas otras razones, generalmente se tiende a limitar F al punto donde la pendiente de la curva del rendimiento por recluta es igual a 1/10 de su valor en el origen (Gulland y Boerema 1973). Este concepto, llamado F0,1, puede ser visto como un sustituto del REM (Rendimiento Económico Máximo), aplicable en situaciones donde los datos económicos sobre la actuación de una pesquería no están disponibles. Un concepto análogo a F0,1, pero aplicado a E es E0,1, que se usa en el Caso III de más arriba.
Otra precaución en el uso de los análisis Y/R es la de siempre examinar la curva correspondiente de biomasa por recluta (B/R o B'/R) calculada con el rendimiento por recluta (se obtiene B/R dividiendo Y/R por F simplemente, véase la ecuación 8 por ejemplo). Aquí, el punto de referencia apropiado es el valor de F (o E) que reduzca B/R (o B'/R) a la mitad de su nivel no-explotado (cuando F o E = 0), es decir, al nivel de biomasa que teóricamente maximiza la producción excedente y permite una ‹ producción máxima equilibrada › (PME, en inglés MSY) (véase Schaefer 1954, 1957 ; Gulland 1983 ; o Pauly 1984). Este nivel se referencia aquí como F0,5 o E0,5 .
Haga clic sobre el botón Biology en la vista SPECIES, y luego sobre el botón Population dynamics en la vista BIOLOGY, y sobre el botón Growth en la ventana POPULATION DYNAMICS. Seleccione un estudio (una linea) y haga click sobre el botón Y/R en la vista POPULATION GROWTH INFORMATION. O bien, usted puede pasar sucesivamente por los botones Reports, Graphs, Population dynamics, Y/R Analyses a partir de la ventana MAIN menu.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Beverton, R.J.H. and S.J. Holt. 1964. Table of yield functions for fishery management. FAO Fish. Tech. Pap. 38, 49 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic methods. FAO/Wiley, New York.
Gulland, J.A. and L. Boerema. 1973. Scientific advice on catch levels. Fish. Bull. (US) 71:325-335.
Jones, R.E. 1957. A much simplified version of the fish yield equation. Doc. No. P. 21. Paper presented at the Lisbon joint meeting of International Commission Northwest Atlantic-Fisheries, International Council for the Exploration of the Sea, and Food and Agriculture Organization of the United Nations. 8 p. [Mimeo].
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish population dynamics in tropical waters: a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and M. Soriano. 1986. Some practical extensions to Beverton and Holt’s relative yield-per-recruit model, p. 491-495. In J.L. Maclean, L.B. Dizon and L.V. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries Society, Manila.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 191, 382 p.
Schaefer, M.B. 1954. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-Am. Trop. Tuna Comm., Bull. 1(2):27-56.
Schaefer, M.B. 1957. A study of the dynamics of the fishery for yellowfin tuna in the eastern tropical Pacific Ocean. Inter-Am. Trop. Tuna Comm., Bull. 2:247-268.
Silvestre, G., M. Soriano and D. Pauly. 1991. Sigmoid selection and the Beverton and Holt equation. Asian Fish. Sci. 4(1):85-98.
Daniel Pauly y Felimon C. Gayanilo, Jr.