Pauly (1986) introdujo un enfoque de estima del consumo de alimento de las poblaciones, que tiene en cuenta la estructura de edad de las poblaciones , definida por:
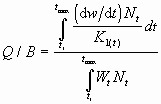 ...1)
...1)
donde
Q/B es el consumo de alimento por unidad de biomasa;
K![]() son los parámetros de la curva de von Bertalanffy o CVB (véase ‹ Dinámica de poblaciones ›, este volumen);
son los parámetros de la curva de von Bertalanffy o CVB (véase ‹ Dinámica de poblaciones ›, este volumen);
es el peso medio a la edad t predicho por la CVB cuya derivada (dw/dt) expresa la tasa de crecimiento;
es el coeficiente de eficacia de conversión del alimento expresado en función de la edad t, asociado a la talla por:
es el número de supervivientes a la edad t en una población de mortalidad Z, como:
exp
indican la edad de reclutamiento y la edad de salida de la población (véase también Palomares y Pauly 1989; 1998).
La ecuación (2) implica
La mortalidad total (Z) de la ecuación (3) es la suma de las mortalidades naturales (M) y por pesquería (F). En las poblaciones inexplotadas, donde F es nula, toda la mortalidad se debe a M. La temperatura del agua es otro parámetro que afecta al metabolismo y al crecimiento de los peces y por tanto al consumo alimentario (Palomares y Pauly 1989 ; Pauly 1989 ; Palomares 1991). Por consiguiente se indica también la Temperatura ambiental (del agua) en °C.
C.
Al igual que en la tabla RATION, existen campos de opciones múltiples Tipo de alimentación (Food type) y Salinidad (Salinity), y un campo textual para la Localidad (Locality). El Tipo de alimentación concierne a los alimentos implicados en la estima de Q/B mediante las siguientes opciones: detritus; plantas; zoobentos; zooplancton; necton; otros. La opción ‹ otros › se usa para las poblaciones que han sido alimentadas de gránulos u otras alimentaciones artificiales. Anotaciones (Remarks) contiene los detalles adicionales.
El hábitat de la población se indica primero a partir del tipo de Salinidad (Salinity), agua de mar, agua salobre o agua dulce, y luego por Localidad (Localidad) y País (Country).
Un gráfico presenta la curva Q/Ben función de W¥
(véase Fig. 33).
Haga clic sobre el botón Biology en la vista SPECIES, y luego sobre el botón Trophic Ecology en la vista BIOLOGY y el botón Food consumption en la vista TROPHIC ECOLOGY. Haga doble clic sobre una de las líneas en la vista FOOD CONSUMPTION para mostrar las informaciones relativas al Q/B designado.
El desarrollo futuro de esta tabla podría implicar las mejoras de la ecuación (2) sugeridas por Temming (1994). Además, nosotros pensamos que un aumento del número de registros de Q/B podría poner en evidencia las relaciones generales, mejorando las propuestas por Pauly (1989), Palomares (1991) o Palomares y Pauly (1998).
Palomares, M.L.D. 1991. La consommation de nourriture chez les poissons: étude comparative, mise au point d’un modèle predictif et application à l’étude des réseaux trophiques. Ecole Nationale Supérieure, Institut National Polytechnique de Toulouse. 211 p. PhD thesis.
Palomares, M.L. and D. Pauly. 1989. A multiple regression model for predicting the food consumption of marine fish populations. Aust. J. Mar. Freshwat. Res. 40:259-273.
Pauly, D. 1986. A simple method for estimating the food consumption of fish populations from growth data and food conversion experiments. Fish. Bull. 84(4):827-839.
Pauly, D. 1989. Food consumption by tropical and temperate marine fishes: some generalizations. J. Fish Biol. 35 (Supplement A):11-20.
Temming, A. 1994. Food conversion deficiency and the von Bertalanffy growth function. Part I. A modification of Pauly’s model. Naga, ICLARM Q. 17(1):38-39.
![]()
![]()
![]() = 1 -
= 1 - ![]() ...2)
...2)
![]()
![]() =
= ![]() ·
·![]()
![]()
![]()
![]() = 0 a
= 0 a ![]() , momento en el cual la alimentación se usa solamente para el mantenimiento (maintenance Q/B) y no más para su crecimiento. Nótese que la mayoría de las estimas de la talla asintótica publicados en la literatura se refieren a la longitud L¥
. Una relación talla-peso, traducida por la constante b (a menudo fijada a 3 en ausencia de una gama suficiente de pares de datos L/W) se usa a menudo para estimar
, momento en el cual la alimentación se usa solamente para el mantenimiento (maintenance Q/B) y no más para su crecimiento. Nótese que la mayoría de las estimas de la talla asintótica publicados en la literatura se refieren a la longitud L¥
. Una relación talla-peso, traducida por la constante b (a menudo fijada a 3 en ausencia de una gama suficiente de pares de datos L/W) se usa a menudo para estimar ![]() a partir de
a partir de ![]() (véase ‹ Dinámica de poblaciones ›, este volumen).
(véase ‹ Dinámica de poblaciones ›, este volumen).
Z = F + M
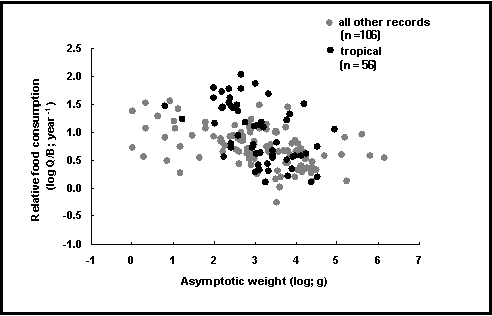
Fig. 33. Consumo relativo de alimento en peces tropicales (puntos negros) comparado con el de otras especies.
Cómo proceder
Bibliografía