Esta tabla contiene las informaciones sobre el crecimiento, la mortalidad natural y la longitud en la madurez, que sirven de parámetros en muchos modelos de evaluación de los stocks de peces. Los datos también pueden ser usados para establecer las relaciones empíricas entre los parámetros de crecimiento o los valores de mortalidad natural estimados, y otros parámetros (por ejemplo, la forma del cuerpo, la temperatura, etc.). Esta es una vía de investigación útil para la evaluación de los stocks y para comprender cada vez mejor la evolución de las estrategias de vida (véase Fig. 16).
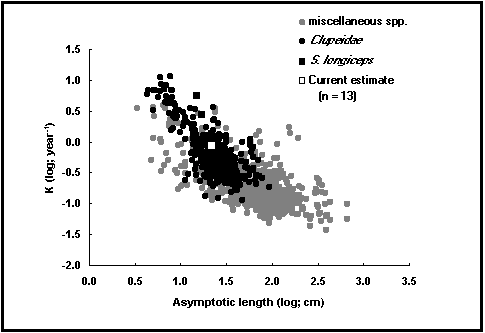
Fig. 16. Nube auximétrica para Sardinella longiceps y el 20% de los datos de otras especies.
Los parámetros de crecimiento contenidos en esta tabla son los de la curva de von Bertalanffy (CVB ; von Bertalanffy 1938), que para el crecimiento en longitud se expresa de la siguiente forma:
![]() ...1)
...1)
donde Lt es la longitud media predicha para un individuo de una población determinada a la edad t, L¥, su longitud asintótica media, es decir la longitud que tendrían en una edad infinita, K, un coeficiente de crecimiento de dimensión tiempo?1, y t0, la edad teórica (y generalmente negativa) para una longitud nula, obtenida por extrapolación de la CVB.
Correlativamente, la CVB para el crecimiento en peso se expresa de la siguiente forma:
donde Wt y W¥ son los pesos correspondientes respectivamente a las Lt y L¥, y b, el coeficiente extraido de una relación talla-peso de tipo:
W = a
POPGROWTH contiene los registros para los cuales están disponibles por lo menos L¥ y K; t0 puede no estar disponible (este parámetro no-biológico no se requiere en la mayoría de los modelos de evaluación de los stocks).
![]() ...2)
...2)
![]() ...3)
...3)
Aproximadamente, la tabla contiene en la actualidad 4 700 juegos de parámetros de crecimiento estimados para 1 150 especies, extraidos de 2 000 fuentes primarias y secundarias. Las recopilaciones de Pauly (1978, 1980) constituyen alrededor de un tercio de estos registros.
Además del campo MainRef., un campo Ref. está asociado a cada conjunto de parámetros de crecimiento, pues en los artículos son a menudo publicados sin los datos que han sido usados para su cálculo. Los datos fuente se indican mediante las siguientes opciones : bandas de crecimiento en otolitos ; bandas en escamas ; otras marcas anuales; anillos diarios de otolito; marcación/recaptura ; distribución de frecuencias de longitud ; observación directa ; diversos tipos de datos ; otros.
El método usado para cada conjunto de parámetros de crecimiento estimado se indica mediante las siguientes opciones : método de Ford-Walford ; método de von Bertalanffy/Beverton ; método de Gulland y Holt ; regresión no-lineal ; ELEFAN I ; otro(s) método(s).
Las descripciones de estos métodos, de sus hipótesis subyacentes, de la conformidad de los datos y de sus sesgos pueden ser encontradas en Bougis (1976), Ricker (1980), Gulland (1983), Pauly (1984 ; 1997), Gayanilo y Pauly (1997), y otras publicaciones pesqueras.
Los campos siguientes permiten verificar resumidamente la exactitud de los parámetros de crecimiento :
un campo calculado contiene el índice de actuación del crecimiento ø' = log10K + 2log10L¥ (Pauly 1979 ; Pauly y Munro 1984 y véase ‹ Análisis Auximétricos ›, este volumen), que puede ser comparado con los valores de ø' de stocks de la misma especie o de una especie estrechamente emparentada;
un campo de opciones múltiples indica el método de cálculo de W¥ en función de L¥ mediante las siguientes opciones:
Como se indica en MainRef. o Ref. para el crecimiento;
Usando la relación L/W del mismo stock;
Usando la relación L/W de un stock diferente de la misma especie;
Usando la relación L/W de una especie similar;
Otros (véase Comments).
Un campo sí/no indica los casos donde L¥ es diferente de Lmax (en la tabla SPECIES) en más de un 30% de Lmax;
Cuando más de 4 registros están disponibles, un campo indica si el par de valores W¥-K se situa fuera de la elipse auximétrica (véase ‹ Análisis Auximétricos ›, este volumen) definida por los otros pares W¥ - K para la especie en cuestión;
Haga clic sobre el botón ‹ gráfico › Growth curves en la tabla resumen para mostrar las curvas de la longitud en función de la edad relativa (= edad real - t0) (Fig. 17). Esta rutina puede ser usada para reparar en las curvas de crecimiento que se desvían de la tendencia general;
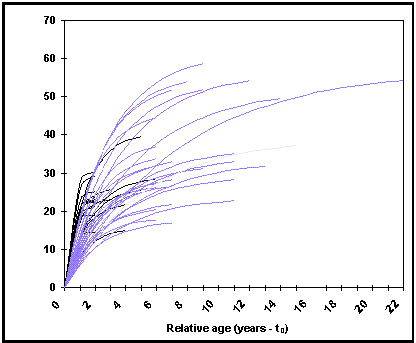
Fig. 17. Longitud en función de la edad relativa (t-t0) para Oreochromis niloticus niloticus. Estas curvas son calculadas por aplicación de los parámetros L¥ y K de la tabla POPGROWTH a la CVB (Ecuación 1). Las curvas de crecimiento asintótico débil corresponden sobretodo a los crecimientos en cautividad (véase Recuadro 15 y Fig. 18).
Haga clic sobre los dos botones ‹ gráficos › siguientes para mostrar las curvas auximétricas, correspondientes respectivamente a logK en función de logL¥ (véase Fig. 16) y de W¥ (véase ‹ Análisis Auximétricos ›, este volumen);
Un campo indica si el conjunto de los parámetros de crecimiento han sido medidos sobre individuos que viven en ‹ aguas libres › o en ‹ cautividad › (véase Recuadro 15 y Fig. 18).
Las informaciones sobre la longitud en la primera madurez (Lm), contenidas en una tabla separada (MATURITY), son usadas conjuntamente con L¥ para calcular la ‹ carga reproductora › (Cushing 1981) de la población, es decir la proporción Lm/L¥. La mayoría de los valores Lm corresponden a una longitud media o a la longitud a la cual el 50% de la población es madura. Pero cuando estos valores no han sido precisados en las publicaciones, o no pueden ser calculados a partir de los datos, Lm es la media de los dos valores límite.
En aguas libres, las condiciones ambientales (por ejemplo, la temperatura, pero también la presencia de depredadores), hacen que los peces crezcan lentamente hasta una gran talla (K débil, L ¥ elevada), o rápidamente hacia una pequeña talla (K elevada, L ¥ débil). Por consiguiente, el índice de actuación de crecimiento (ø' = logK + 2 logL ¥) permanece casi constante entre las diferentes poblaciones de una misma especie (Pauly 1994). Las razones de esta constancia de ø', que en el fondo se debe a la manera en que los peces reparten el uso del poco oxígeno que se difunde a través de sus branquias, son discutidas por Pauly (1981, 1994).
Para la mayoría de los peces que viven en cautividad, la ausencia de depredadores y de competidores sexuales permite un reparto de oxígeno más importante para la alimentación y el crecimiento, en detrimento de los comportamientos que son costosos en términos de demanda de oxígeno, como la huida frente a los depredadores, o el combate con los competidores sexuales.
Los índices ø' de los individuos mantenidos en cautividad son por consiguiente superiores a los de las poblaciones en medio natural. Además, este efecto aumenta con la sofisticación del sistema de producción (Pauly et al. 1988). Evidentemente, este efecto se refuerza por la mejora genética para el crecimiento. Por ejemplo, en Oreochromis niloticus (tilapia del Nilo) (Pullin 1988) o Salmo salar (salmón Atlántico) (Gjedrem 1985), la selección de los individuos más tranquilos, aunque a menudo involuntaria, favorece un reparto optimo del oxígeno para el crecimiento (Jones 1996 ; Bozynski 1998).
Estos efectos combinados resultan en valores de ø' superiores para los individuos cultivados en los sistemas intensivos que para sus congéneres que viven en aguas libres. Se desarrolló un gráfico para evidenciar estos efectos, gracias a la introducción de un campo en la tabla POPGROWTH que distingue los dos tipos de condición de vida.
Como puede observarse sobre la curva auximétrica de la figura 18, los puntos referidos a los peces que viven en cautividad se desvían bastante de los referidos a sus congéneres salvajes, sobretodo para los valores de L¥ comprendidos entre 10 y 30 cm que corresponden principalmente a los de O. niloticus cultivados en sistemas intensivos.
Bibliografía
Bozynski, C.C. 1998. Interactions between growth, sex, reproduction, and activity levels in control and fast-growing strains of Nile tilapia (Oreochromis niloticus). Department of Zoology, University of British Columbia. Master thesis. 109 p.
Gjedrem, T. 1985. Improvement of productivity through breeding schemes. Geo J. 10(3):233-241.
Jones, R.E. 1996. Comparison of some physical characteristics of salmonids under culture conditions using underwater video imaging techniques. University of British Columbia. Master thesis. 104 p.
Pauly, D. 1981. The relationships between gill surface area and growth performance in fish: a generalization of von Bertalanffy's theory of growth. Meeresforschung 28(4):251-282.
Pauly, D. 1994. On the sex of fish and the gender of scientists: essays in fisheries science. Chapman and Hall, London. 250 p.
Pauly, D., J. Moreau and M. Prein. 1988. Comparison of growth performance of tilapia in open water and aquaculture, p. 469-479. In R.S.V. Pullin, T. Bhukaswan, K. Tonguthai and J.L. Maclean (eds.) Proceedings of the Second International Symposium on Tilapia in Aquaculture, 16-20 March 1987, Bangkok, Thailand. ICLARM Conf. Proc. 15.
Pullin, R.S.V., Editor. 1988. Tilapia genetics for aquaculture. ICLARM Conf. Proc. 16, 108 p.
Daniel Pauly
Para algunos registros, las estimas de L ¥ deben todavía compararse con la longitud máxima registrada (Lmax) que debería ser a priori razonablemente parecida (véase más arriba).
Nosotros esperamos los comentarios de los usuarios sobre el contenido y/o la utilidad de la tabla POPGROWTH con impaciencia.
Haga clic sobre el botón Biology en la vista SPECIES, y luego sobre el botón Population dynamics en la vista BIOLOGY, y sobre el botón Growth en la ventana POPULATION DYNAMICS. La Fig. 18 también se obtiene haciendo clic sobre el botón Reports en la ventana MAIN menu y luego sobre el botón Population dynamics en la ventana GRAPHS menu.
Cushing, D.H. 1981. Fisheries biology: a study in population dynamics. 2nd ed. University of Wisconsin Press, Madison. 295 p.
Froese, R. and C. Binohlan. 2000. Empirical relationships to estimate asymptotic length, length at first maturity and length at maximum yield per recruit in fishes, with a simple method to evaluate length frequency data. J. Fish Biol. 56:758-773.
Gayanilo, F.C., Jr and D. Pauly. 1997. The FAO-ICLARM Stock Assessment Tool (FiSAT). Reference Manual. FAO Comp. Inf. Ser./Fish. 8, 262 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic methods. FAO/Wiley, New York.
Pauly, D. 1978. A preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 63, 156 p.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish population dynamics in tropical waters: a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and J.L. Munro. 1984. Once more on growth comparison in fish and invertebrates. Fishbyte 2(1):21.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 191, 382 p.
von Bertalanffy, L. 1938. A quantitative theory of organic growth. (Inquiries on growth laws II). Hum. Biol. 10:181-213.
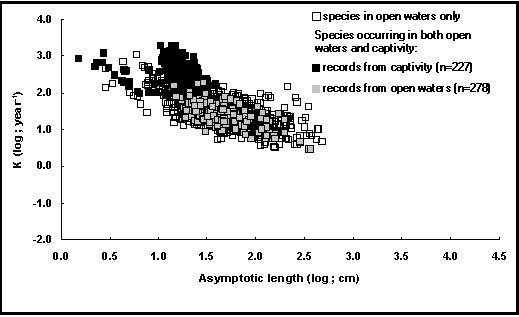
Fig. 18. Nube auximétrica que muestra el crecimiento de los peces en cautividad. Los cuadros negros cuyo log(L ¥) está comprendido entre 1,0 y 1,5 corresponden principalmente a los Oreochromis niloticus cultivados en sistemas intensivos y semi-intensivos (véase Recuadro 15).
Cómo proceder
Bibliografía