Que el crecimiento de los peces presenta oscilaciones estacionales era un hecho bien conocido por los pioneros de la biología de las pesquerías, particularmente T.W. Fulton (1901, 1904) que inventó el análisis de las frecuencias de longitud con C.G.J. Petersen.
Este conocimiento pasó a un segundo plano pues los científicos pesqueros abandonaron gradualmente el análisis de las longitudes en favor de los estudios de las bandas de crecimiento (sobre los otolitos, las escamas y huesos) para estimar las tasas y trazar las curvas de crecimiento (Went 1972). De esta manera, en su clásica obra de 1957, Beverton y Holt no trataron las oscilaciones estacionales del crecimiento más allá de una simple curiosidad académica, y particularmente, no encontraron ninguna razón para modificar la ecuación de la curva de von Bertalanffy (CVB) para tener en cuenta esas oscilaciones, aunque ocurren en todos los peces que estudiaron.
Después de que von Bertalanffy y Müller hubieran evocado el crecimiento estacional en 1943, Ursin fue el primero en publicar una CVB que tenía en cuenta estas oscilaciones (1963a, 1963b). Otras modificaciones fueron propuestas (Pitcher y MacDonald 1973 ; Daget y Écoutin 1976), pronto seguidos por una sucesión de mejoras de estos modelos (Cloern y Nichols 1978 ; Pauly y Gaschütz 1979 ; Appeldoorn 1987 ; Somer 1988 ; Soriano y Pauly 1989). Los ejemplos de aplicación presentados por estos autores pusieron en evidencia que los modelos de crecimiento que no consideran explícitamente las oscilaciones estacionales omiten un aspecto esencial del proceso de crecimiento (Pauly 1990, 1994).
Esto también es válido para peces tropicales, pues la poca diferencia de temperatura de 2°C entre invierno y verano es suficiente para inducir oscilaciones estacionales de crecimiento que son estadísticamente significativas aunque visualmente indetectables (Pauly e Ingles 1981 ; Longhurst y Pauly 1987).
El modelo de crecimiento que mejor tiene en cuenta las oscilaciones estacionales de crecimiento es probablemente el de Somer (1988), con la expresión siguiente
Lt = L¥ {1 – exp – [ K (t – t0) + S(t) – S(t0)]} …1)
donde
L¥ , K and t0 se definen como en la CVB estándar se definen como en la CVB estándar;
S(t) = (CK/2p ) Sin p (t – t
s); and
S(t0) = (CK/2p ) Sin p (t0 - t
s).
La ecuación (1) tiene dos parámetros más que la CVB estándar: C y ts. C expresa la amplitud de las oscilaciones de crecimiento y es la más facil de interpretar. Cuando C = 0, la ecuación (1) pasa a ser la CVB estándar ; cuando C = 0,5, las oscilaciones estacionales de crecimiento son tales que el crecimiento se incrementa un 50% en el pico de crecimiento del verano, y, brevemente, se reduce un 50% en invierno. Cuando C = 1, el crecimiento se incrementa un 100%, es decir, que se dobla en verano y se hace nulo en invierno (véase Fig. 21).
El segundo nuevo parámetro, ts, corresponde a la duración entre t=0 y el inicio de una oscilación sinusoidal de crecimiento. Para la visualización, es útil definir un ‹ punto invernal › (o Winter Point) WP = ts + 0,5 que expresa como una fracción del año el periodo donde el crecimiento es más lento. WP es a menudo cercano a 0,1 en el hemisferio norte (es decir a mediados de febrero) y a 0,6 en el hemisferio sur (mediados de agosto), de ahí su nombre. [Nótese que la alternancia de temperaturas estivales altas e invernales bajas no es necesariamente la causa de las oscilaciones estacionales de crecimiento ; en los peces de agua dulce del Amazonas, por ejemplo, estas oscilaciones son debidas a la alternancia de las estaciones de inundación y las secas. Nótese también que la ecuación (1) no puede describir largos periodos de crecimiento nulo (ni utilizar valores de C > 1), problema discutido por Pauly et al. (1992)].
Como este modelo y sus predecesores (particularmente el modelo de Pauly y Gaschütz 1979) han sido adaptados a numerosos datos de oscilaciones estacionales de crecimiento, las evaluaciones de C están disponibles para una amplia gama de especies y de hábitats.
La tabla POPGROWTH incluye la mayoría de las evaluaciones de C publicadas para los peces, junto con las evaluaciones de la diferencia de temperatura verano-invierno (DT ; diferencia de los valores medios mensuales, en °C). Como puede observarse en la figura 22, estos valores de C aumentan con DT, para un valor de C cercano a 1 cuando DT está alrededor de 10°C.
Algunas de las implicaciones fisiológicas de esta relación, conocidas desde el principio de los años 1980 (véase por ejemplo, Pauly e Ingles 1981), son discutidas por Longhurst y Pauly (1987).
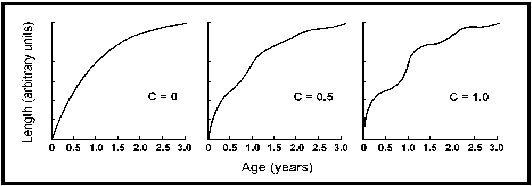
Fig. 21. Efecto del parámetro de amplitud C sobre una curva de von Bertalanffy con L¥ = 25 unidades, K = 1 año?1, t0 = 0 y ts = 0.
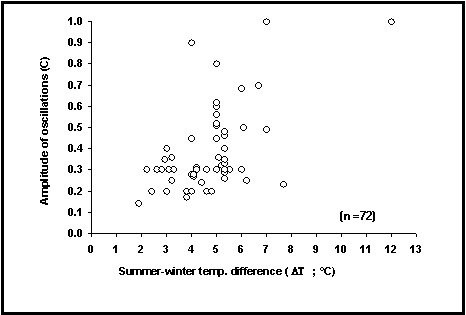
Fig. 22. Relación entre el parámetro C y las diferencias de temperatura verano-invierno de su hábitat (DT en °C) para 72 poblaciones de peces. C refleja la amplitud de las oscilaciones estacionales de crecimiento.
Para mostrar el gráfico de la figura 22, haga clic sobre el botón Reports en la ventana MAIN menu, luego sobre el botón Graphs en la ventana PREDEFINED REPORTS, el botón Population dynamics en la ventana GRAPHS, y el botón Seasonal growth en la ventana POPULATION DYNAMICS.
Appeldoorn, R. 1987. Modifications of a seasonal growth function for use with mark-recapture data. J. Cons CIEM 43:194-198.
Bertalanffy, L. von and I. Müller. 1943. Untersuchungen über die Gesetzlichkeit des Wachstums. VIII. Die Abhängigkeit des Stoffwechsels von der Korpergrösse und der Zusammenhang von Stoffwechseltypen und Wachstumstypen. Rev. Biol. 35:48-95.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Cloern, J.E. and F.H. Nichols. 1978. A von Bertalanffy growth model with a seasonally varying coefficient. J. Fish. Res. Board Can. 35:1479-1482.
Daget, J. and J.M. Ecoutin. 1976. Modéles mathématiques de production applicables aux poissons tropicaux subissant un arrêt annuel prolongé de croissance. Cah. ORSTOM, sér. Hydrobiol. 10(2):59-69.
Fulton, T.W. 1901. The rate of growth of the cod, haddock, whiting and Norway pout. 19th Ann. Rep. Fish. Board Scotland. Part III:154-228.
Fulton, T.W. 1904. The rate of growth of fishes. 22nd Ann. Rep. Fish. Board Scotland. Part III:141-240.
Longhurst, A.R. and D. Pauly. 1987. Ecology of tropical oceans. Academic Press, San Diego, California. 407 p.
Pauly, D. 1990. Length-converted catch curves and the seasonal growth of fishes. Fishbyte 8(3):33-38.
Pauly, D. and G. Gaschütz. 1979. A simple method for fitting oscillating length growth data, with a program for pocket calculators. I.C.E.S. CM 1979/6:24. Demersal Fish Cttee, 26 p.
Pauly, D. and J. Ingles. 1981. Aspects of the growth and natural mortality of exploited coral reef fishes, p. 89-98. In E.D. Gomez, C.E. Birkeland, R.W. Buddemeyer, R.E. Johannes, J.A. Marsh and R.T. Tsuda (eds.) The reef and man. Proceedings of the Fourth International Coral Reef Symposium. Vol. 1, Marine Science Center, University of the Philippines, Quezon City.
Pauly, D., M. Soriano-Bartz, J. Moreau and A. Jarre. 1992. A new model accounting for seasonal cessation of growth in fishes. Aust. J. Mar. Freshwat. Res. 43:1151-1156.
Pitcher, T.J. and P.D.M. MacDonald. 1973. Two models for seasonal growth in fishes. J. Appl. Ecol. 10:599-606.
Somer, I.F. 1988. On a seasonally oscillating growth function. Fishbyte 6(1):8-11.
Soriano, M. and D. Pauly. 1989. A method for estimating the parameters of a seasonally oscillating growth curve from growth increments data. Fishbyte 7(1):18-21.
Ursin, E. 1963a. On the incorporation of temperature in the von Bertalanffy growth equation. Medd. Danm. Fisk. Havunders. N.S. 4(1):1-16.
Ursin, E. 1963b. On the seasonal variation of growth rate and growth parameters in Norway pout (Gadus esmarki) in Skagerrak. Medd. Danm. Fisk. Havunders. N.S. 4(2):17-29.
Went, A.E.J. 1972. Seventy years agrowing: a history of the International Council for the Exploration of the Sea, 1902-1972. Rapp. P.-V. Réun. CIEM 165. 252 p.
Daniel Pauly