En pesquerías, las mortalidades se expresan generalmente en forma de tasas instantáneas, es decir:
![]() …1)
…1)
donde N0 y N1 son los efectivos consecutivos de una población afectados por una tasa (total) de mortalidad Z durante un intervalo de tiempo Dt.
Eso permite definir
Z = F + M ...2)
donde F es la mortalidad por pesquería y M la mortalidad natural, causada por cualquier factor ajeno a la pesquería (en un stock inexplotado, obviamente Z = M).
Las estimas de la mortalidad natural son generalmente difíciles de obtener (con la excepción de las poblaciones no-explotadas, que suelen ser inaccesibles para el estudio y cada vez son más raras). Así pues, prácticamente todas las estimas de M bien documentadas en la literatura han sido incorporadas en la tabla POPGROWTH, que contiene actualmente más de 400 estimas de mortalidad natural para más de 200 especies (véase Recuadro 17). Alrededor del 42% de estos registros han sido extraidos de Pauly (1980 ; véase igualmente los ‹ Análisis de rendimiento por recluta ›, este volumen), y el 21% de Beverton y Holt (1959) y Djabali et al. (1993).
Los gráficos de FishBase sobre la mortalidad natural están calculados a partir de lo que seguramente es la mayor recopilación mundial de estimas independientes de mortalidad natural de peces. No existen otros datos similares que pudieran ser usados para verificar las generalizaciones derivadas de este conjunto de datos. Como la reproducción de nuestros resultados de manera independiente es pues difícil, conviene ser muy prudentes en la presentación de las generalizaciones basadas en este conjunto de datos.
Por consiguiente nosotros estamos aquí limitados a dos gráficos que verifican las generalizaciones anteriores de Beverton y Holt (1959) y Pauly (1980). La Fig. 23 muestra los logM en función de logK, los parámetros de curvatura de la CVB. Como puede observarse, confirma que K, que está asociada a la longevidad, es un buen indicador de M. La varianza es alta de todas maneras, lo que sugiere que otros factores pueden influenciar a M.
La Fig. 24 ilustra otros dos factores que influencian a M, el tamaño (aquí una longitud) y la temperatura del ambiente. Muestra los logM en función de logL ¥ para los peces que viven en temperaturas inferiores a 20°C (puntos abiertos ; alrededor de 2/3 de todos los casos), y para los peces tropicales (puntos llenos).
Como puede observarse, M no está solamente asociada a L¥ (y a K ; véase Fig. 23), también lo está a la temperatura. No obstante, Charnov (1993), en contradicción manifiesta con los datos actualmente disponibles, presenta unos conceptos de ‹ invariantes de Beverton y Holt ›, de los cuales la relación M/K se supone forma parte de ellos, que no permiten poner en evidencia los efectos de la temperatura.
Bibliografía
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O’Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol 5, J. & A. Churchill Ltd., London.
Charnov, E. 1993. Life-history invariants: some explorations of symmetry in evolutionary ecology. Ecology and Evolution. Oxford University Press, Oxford. 128 p.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly
Nótese que estos valores son todos independientes, es decir que no fueron evaluados usando métodos o modelos empíricos que asocian los valores de M con variable(s) de predicción, como expresa Pauly (1980). De esta manera, las estimas de M presentadas aquí pueden ser usadas para definir nuevos modelos empíricos.
Dada la importancia de este parámetro, parece útil proporcionar una estima de temperatura ambiental media (en °C) para cada registro de la tabla POPGROWTH que contenga un valor de M. El método usado para estimar M se precisa mediante las siguientes opciones : curva de capturas en un stock inexplotado ; longitud media para un stock inexplotado ; marcación y recaptura ; curva de Z en función del esfuerzo de pesquería ; curva parabólica de Z en función de las capturas ; modelo Ecopath (Christensen y Pauly 1993) ; otro método.
Estas técnicas se describen en los manuales de referencia citados en ‹ La tabla POPGROWTH › (este volumen), salvo el modelo Ecopath, brevemente descrito en el Recuadro 19.
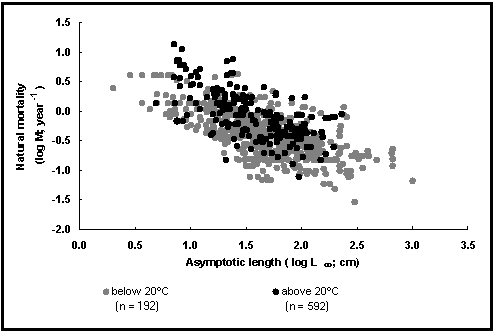
Fig. 24. Mortalidad natural en función de la longitud asintótica para los peces tropicales (círculos llenos) y otros peces (círculos abiertos). Nótese el efecto de la temperatura. Véase Recuadro 17 para más detalles.
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O’Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol. 5, J. & A. Churchill Ltd., London.
Christensen, V. and D. Pauly, Editors. 1993. Trophic models of aquatic ecosystems. ICLARM Conf. Proc. 26, 390 p.
Djabali, F., A. Mehailia, M. Koudil and B. Brahmi. 1993. Empirical equations for the estimation of natural mortality in Mediterranean teleosts. Naga, ICLARM Q. 16(1):35-37.
Froese, R., C. Binohlan and D. Pauly. Empirical equations to estimate natural mortality in fishes. (In prep.).
Hoenig, J. 1984. Empirical use of longevity data to estimate mortality rates. Fish. Bull. (US) 81(4): 898-903.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly y Crispina Binohlan