Durante el proceso de crecimiento de los peces, el tamaño (expresado por un peso o una longitud) varía con el tiempo. Cualquier intento de representar o comparar los crecimientos debe tratar estas dos dimensiones. De todas maneras, comparar las curvas de crecimiento, que asocian la talla al tiempo, no es tan simple. En efecto, dependiendo de la definición aceptada de los crecimientos ‹ lento › y ‹ rápido ›, pueden surgir serias contradicciones cuando las curvas de crecimiento se cruzan. Así pues Kinne (1960) escribió que " la diferencia de tasa de crecimiento establecido en peces juveniles no persiste a lo largo de toda su vida. Los peces con un crecimiento inicial lento pueden sobrepasar a los peces con un crecimiento inicial rápido, y finalmente tener una longitud superior en una misma edad. " (este fenómeno está bien ilustrado en la Fig. 17).
En FishBase, usamos los parámetros de la curva de von Bertalanffy o CVB (véase ‹ La tabla POPGROWTH ›, este volumen) para describir el crecimiento de los peces. De todas maneras, eso no resuelve por sí mismo el problema comentado por Kinne (1960), pues ninguno de estos parámetros tiene una dimensión de crecimiento (es decir, unidad de longitud o de peso por unidad de tiempo). L¥ y W¥ no representan más que al tamaño, y K y t0 al tiempo (tiempo?1 y tiempo, respectivamente). De todas maneras, varias combinaciones de estos parámetros, por ejemplo L¥·K, tienen las dimensiones apropiadas (aquí : longitud×tiempo?1), es decir las de una tasa de crecimiento (Gallucci y Quinn 1979). Aunque usando los logaritmos, los índices de actuación de crecimiento:
Ø
’ = logK + 2logL¥ …1)y
Ø
tienen también una dimensión correcta de tasa de crecimiento, y son actualmente ampliamente usados para comparar las actuaciones de crecimiento de los diferentes peces y de los invertebrados, considerando las distribuciones normales (y relativamente estrechas) de las diferentes poblaciones de una misma especie (ver, por ejemplo, Moreau et al. 1986). Esta última característica permite también la estima de K a partir de L ¥ o W¥ cuando su Ø' o Ø Ø (medias) son conocidas para una o varias poblaciones (Munro y Pauly 1983 ; Pauly y Munro 1984).
Las pendientes de 2 y 2/3 respectivamente en las ecuaciones (1) y (2) han sido estimadas por Pauly (1979) a partir de un gran conjunto de datos actualmente incluidos en FishBase (Pauly 1978, 1979). La ecuación (1) implica que las curvas de logK en función de logL¥ tendrán una pendiente de -2 de media, y la ecuación (2), que las curvas de logK en función de logW¥ tendrán una pendiente de -2/3.
Las pendientes de 2 y 2/3 respectivamente en las ecuaciones (1) y (2) han sido estimadas por Pauly (1979) a partir de un gran conjunto de datos actualmente incluidos en FishBase (Pauly 1978, 1979). La ecuación (1) implica que las curvas de logK en función de logL¥ tendrán una pendiente de -2 de media, y la ecuación (2), que las curvas de logK en función de logW¥ tendrán una pendiente de -2/3. Una nube ‹ auximétrica › (de las palabras griegas para ‹ crecimiento › y ‹ medida ›) es un gráfico logarítmico del parámetro K de la CVB en función de la talla asintótica (L¥ o W¥). De esta manera, una población con su conjunto de parámetros de crecimiento (L¥ -K o W¥ -K) se representa por un solo punto, y las diferentes poblaciones de la misma especie tendrían tendencia a ser reagrupadas. Como las ecuaciones (1) y (2) implican que estos grupos deben alinearse a lo largo de las rectas de regresión de pendiente conocida, pueden ser superpuestas por las elipses cuyo eje principal presenten igualmente una pendiente igual a 2 o 2/3, donde los puntos de intersección son iguales a Ø ' o Ø, y donde las superficies corresponden a la varianza de los conjuntos de valores que representan.
Las elipses cuyas superficies contengan el 95% del límite de confianza (S95) de un clúster de pares L¥-K (o W¥-K) pueden ser estimadas fácilmente. El programa AUXIM (Pauly et al. 1996) calcula los S95 para los grupos de por lo menos 4 pares L¥ -K o W¥-K, y dispone de rutinas asociadas.
Como sería tedioso trabajar con AUXIM de forma separada, un subconjunto de sus rutinas fue incluido en FishBase 99 para permitir el análisis del gran número de parámetros de crecimiento que están disponibles. De todas maneras, para permitir comparaciones entre peces de conformaciones muy diferentes, sólo se han incluido las rutinas que pertenecen al crecimiento en peso (y a Ø, no a Ø '). Además, únicamente los peces que viven en aguas libres (y no en cautividad) pueden ser incluidos en los análisis (la razón viene explicada en el Recuadro 15).
Los análisis auximétricos se llaman desde la ventana REPORTS, después de haber identificado un grupo de especies (por ambiente o por taxon supra-específico, orden, familia o género). Un análisis auximétrico completo comprende:
muestra de un gráfico donde se trazan todas las elipses de las especies seleccionadas que tengan por lo menos 4 datos (véase Fig. 19 ; Recuadro 16), y muestra de las estimas de los valores medios de K y W¥;
estima y muestra en forma de tabla de las distancias y de los solapamientos entre especies (para un mínimo de 4 especies); y
aplicación del algoritmo de aglomeración de McCammon y Wenninger (1970) en las distancias calculadas en (b) para construir un dendrograma en ‹el espacio de crecimiento ›, y mostrar así las similaridades de crecimiento entre las especies del grupo seleccionado (Fig. 19).
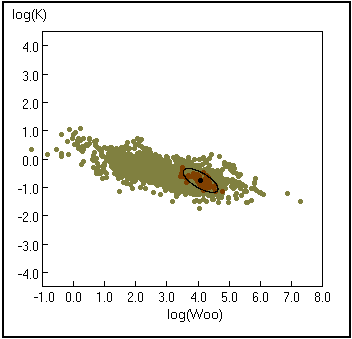
Fig. 19. Curva de K en función de W¥. Los puntos claros representan todas las especies para las cuales W¥ está disponible en FishBase. Los puntos oscuros representan los registros para Gadus morhua. La elipse, con un punto negro en su centro representa el 95% del límite de confianza. Véase Recuadro 16 para los detalles.
Analisis como estos han sido hasta ahora tansolo efectuados para las tilapias, familia de los Cichlidae (Pauly et al. 1996) y los pargos, familia de los Lutjanidae (Pauly y Binohlan 1996). Su potencial no ha sido pues totalmente explorado. Confiamos en que estos análisis extenderán considerablemente la comprensión del crecimiento, y más generalmente, de la biología de los peces. Nosotros esperamos las reacciones de los usuarios con impaciencia.
Este texto, cuya primera parte está adaptada de Pauly et al. (1996), resume las características esenciales del enfoque usado en AUXIM para calcular las elipses. Conocido el peso CVB, y la definición de Ø, nosotros tenemos
que es la ecuación del eje mayor de la elipse, Ø siendo el punto de intersección con la ordenada.
Simultáneamente, y puesto que es perpendicular, la ecuación para el eje menor es
donde Yo es la ordenada del punto de intersección con el eje de las ordenadas. La abscisa del punto de intersección del eje menor con el eje de la abscisa es
Si una elipse debe hacer referencia al 95% del límite de confianza de una nube de puntos, la longitud del eje mayor (2 . a) debe estar relacionada con la desviación típica de Xo ; de la misma forma, la longitud del eje menor (2 . b) debe estar relacionada con la desviación típica de Ø, es decir
donde el valor de t depende del número de puntos (n), con t = 1.96 cuando n = ¥ (Sokal y Rohlf 1995), y donde el factor (3/2) · (1/ ((1 + (3/2)2)1/2) tiene en cuenta el hecho de que los ejes de las elipses no sean paralelos al eje del sistema de coordenadas.
Cuando las elipses hacen referencia a la desviación típica de los valores medios de logW¥
y logK, sd(Xo) and sd(Ø) se reemplazan por los errores estándares, es decir, respectivamente por se(Xo) y se(Ø).
Cómo usar AUXIM:
La interfaz usuario de AUXIM tiene cuatro partes:
Los botones de comandos en la esquina superior izquierda de la pantalla sirven para : (i) aumentar o disminuir la talla de la curva auximétrica (es decir más o menos zoom) ; (ii) abrir la lista de especies seleccionada antes de la activación de la rutina principal de AUXIM (haga clic sobre el botón Reports en la ventana MAIN menu, y luego sobre el botón Graphs, el botón Population dynamics, y el botón Auximetric analysis);
Muestra de las especies seleccionadas y de los botones que permiten un paseo por la lista (esquina superior derecha de la pantalla);
Muestra de la curva auximétrica, permitiéndose también la visualización de la tabla de distancias y solapamientos, y el dendrograma; y
Los botones del sistema de comandos para : (i) seleccionar o deseleccionar una especie de la lista ; (ii) imprimir la visualización actual o salvaguardar en un fichero imprimible ; (iii) abrir el fichero de ayuda ; o (iv) cerrar la ventana y volver a FishBase
Nótese que las funciones asociadas a los botones de comando son accesibles haciendo clic sobre el botón derecho del ratón. Además, una especie puede ser seleccionada o deseleccionada en la lista bien haciendo doble clic sobre la especie, o presionando la barra de espacio.
Pauly, D., J. Moreau and F.C. Gayanilo, Jr. 1996. A new method for comparing the growth performance of fishes, applied to wild and farmed tilapias, p. 433-441. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (eds.) The Third International Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Sokal, R.R. and F.J. Rohlf. 1995. Biometry. Third edition. W.H. Freeman and Company, San Francisco. 887 p.
Daniel Pauly and Felimon C. Gayanilo, Jr.
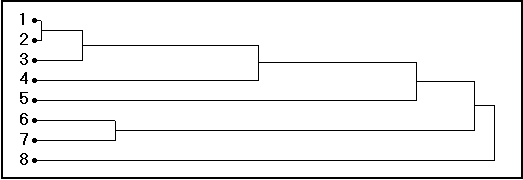
Fig. 20. Dendrograma de similaridades (eje-X en unidades arbitrarias) en ‹ el espacio de crecimiento › definido por AUXIM para los Gadidae, con 1 = Theragra chalcogramma; 2 = Trisopterus luscus; 3 = Merlangius merlangus; 4 = Micromesistius poutassou; 5 = Melanogrammus aeglefinus; 6 = Gadus morhua; 7 = Pollachius virens; 8 = Trisopterus minutus. Como puede constatarse, Theragra chalcogramma y Trisopterus luscus por una parte, y G. morhua y P. virens por otra, forman 2 grupos bien separados, aglomerándose las otras especies sucesivamente.
Gallucci, V.F. and T.J. Quinn, II. 1979. Reparameterizing, fitting, and testing a simple growth model. Trans. Am. Fish. Soc. 108(1):14-25.
Kinne, O. 1960. Growth, food intake, and food consumption in an europlastic fish exposed to different temperatures and salinities. Physiol. Zool. 33:288-317.
McCammon, R.B. and G. Wenninger. 1970. The dendrograph. Computer Contribution 48. State Geological Survey. The University of Kansas, Lawrence. 26 p.
Moreau, J., C. Bambino and D. Pauly. 1986. A comparison of four indices of overall fish growth performance, based on 100 tilapia populations (Fam. Cichlidae), p. 201-206. In J.L. Maclean, L.B. Dizon and L.V. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries Society, Manila, Philippines.
Munro, J.L. and D. Pauly. 1983. A simple method for comparing the growth of fishes and invertebrates. Fishbyte 1(1):5-6.
Pauly, D. 1978. A preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 63, 156 p.
Pauly, D. and J.L. Munro. 1984. Once more on the comparison of growth in fish and invertebrates. Fishbyte 2(1):21.
Pauly, D. and C. Binohlan. 1996. FishBase and AUXIM as tools for comparing the life-history patterns, growth and natural mortality of fish: applications to snappers and groupers, p. 223-247. In F. Arreguin-Sánchez, J.L. Munro, M.C. Balgos and D. Pauly (eds.) Biology, fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. 48.
Pauly, D., J. Moreau and F.C. Gayanilo, Jr. 1996. A new method for comparing the growth performance of fishes, applied to wild and farmed tilapias, p. 433-441. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon-Kothias and D. Pauly (eds.) The Third International Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Daniel Pauly, Jacques Moreau y Felimon C. Gayanilo, Jr.