Uma das razões principais que leva os cientistas a estudar o crescimento dos peixes e a descrevê-lo através da função de crescimento de von Bertalanffy (CVB), é para fazer avaliações de stocks utilizando o modelo de rendimento por recruta (Y/R) de Beverton & Holt (1957) ou uma das suas variantes.
Assim, para optimizar o uso dos parâmetros CVB, foi incluído um botão Y/R na tabela POPCRESCIMENTO que, quando pressionado, possibilita a a realização de diversas análises de rendimento por recruta, de acordo com as entradas da tabela e as escolhas do utilizador. Para ver as definições de alguns dos termos utilizados abaixo, consulte os capítulos sobre a tabela POPCRESCIMENTO, MORTALIDADE NATURAL e a tabela COMPRIMENTO-PESO (este volume).
Antes de apresentar as opções disponíveis devem ser definidos os termos "recruta" e "rendimento por recruta". Apesar de a definição variar de acordo com os autores, podemos neste caso considerar como recrutas os juvenis vulneráveis à pesca, cujo crescimento é descrito pela equação CVB e cuja taxa instantânea de mortalidade natural é semelhante à dos adultos. Estes recrutas têm uma idade média tr, um comprimento médio Lr e um peso médio Wr. Quando alcançam a idade tr, os recrutas podem ser capturados imediatamente, caso em que a idade da primeira captura iguala a idade do recrutamento (tc = tr<./sub). Por outro lado, os recrutas podem ser capturados numa idade mais avançada (com um tamanho superior correspondente, Lc e Wc). Neste caso, devido à mortalidade natural, o número de recrutas que entram na fase explorada Rr será inferior do que o número de recrutas inicial Rc, ou
![]()
![]() …1)
…1)
Deste modo, para cada combinação de valores tc e F, existe um rendimento por recruta (Y/R = captura em peso, por recruta) que pode ser estimada a partir de várias equações cuja forma específica depende do modelo utilizado para descrever o crescimento do peixe. Nos parágrafos seguintes, são dadas as equações para a estimativa de Y/R segundo três formas de CVB, isto é,
Caso I: ![]() …2)
…2)
ou CVB padrão, com base na conversão de comprimento utilizando a relação comprimento-peso
![]() …3)
…3)
onde c.f. é o factor condição.
Caso II: ![]() …4)
…4)
que é uma forma especial de CVB onde o expoente (b) da relação comprimento-peso pode tomar valores diferentes de 3, isto é,
![]() …5)
…5)
onde b ¹ 3.
Caso III: ![]() …6)
…6)
que representa o crescimento em comprimento CVB, e que pode ser utilizada para a análise relativa de rendimento por recruta quando a relação comprimento-peso não está disponível.
Estimativa do rendimento por recruta
Caso I é o modelo original de Beverton & Holt (1957), que têm a fórmula::
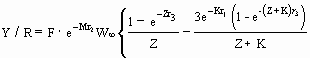
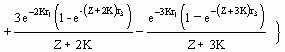 …7)
…7)
onde Z = F + M ;
r1 = tc - t0 ;
r2 = tc - tr ;
r3 = tmax - tc ; y
onde W ¥ , K e t0 são parâmetros de crescimento (veja a tabela "POPCRESCIMENTO", neste vol.), a definição de tc e tr é a mencionada acima e tmáx é "a idade máxima de contribuição para a fase explorada" (Ricker 1975) ou, de forma mais simples, a longevidade do peixe em questão (tal como apresentado na tabela ESPÉCIES). O efeito do valor exacto de tmáx é geralmente pequeno, e assim, quando não é possível encontrar um valor elevado e adequado de tmáx, a Equação (7) pode ser consideravelmente simplificada fazendo tmáx = ¥, neste caso a equação (7) fica:
![]() …8)
…8)
sendo os parâmetros os indicados na equação.
Ambas as equações (7) e (8) podem ser utilizadas para estimar o efeito na rendimento por recruta, de diferentes valores de tc, correspondentes a diferentes valores de Lc , tais como os causados por redes de diferentes tamanhos, e em que F corresponde a diferentes intensidades de pesca.
A rotina gráfica aqui incluída permite visualizar e imprimir dois tipos de gráficos: (a) gráficos Y/R (sempre em g × ano-1) vs F (ano-1), para valores de Lc seleccionados pelo utilizador (Fig. 19), ou (b) "gráficos de isopletas", que apresentam o rendimento por recruta para valores de Lc/L¥ que variam entre 5 e 95% de L¥ , e valores de F desde zero até um limite superior (po defeito 5 ano-1; max. = 20 ano-1) escolhido pelo o utilizador (veja a Fig. 26, e a Caixa 18).
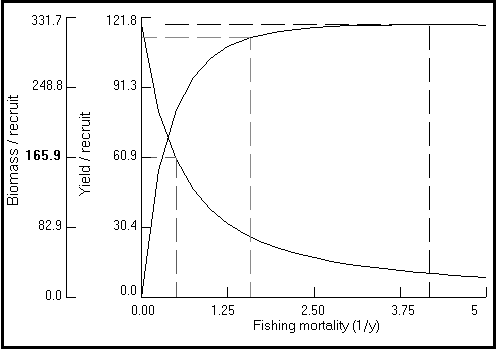
Fig. 25. Curva bi-dimensional de rendimento por recruta para Plectropomus leopardus. Os parâmetros utilizados são: W¥ = 2.220 g; K = 0.43 ano-1; to = 0.34 ano, M = 0.86 ano-1; b = 3.2; tr = 0.12 ano; e tmax = 26 anos. LC foi estimado em 20 cm. As curvas descendentes mostram o declínio de biomassa por recruta (B/R) com o aumento da mortalidade por pesca (F). A curva ascendente ilustra o pequeno aumento de rendimento quando f aumenta para lá de F0,1= 1,75 ano-1. As unidades estão em gramas para B/R e em gramas/ano para Y/R. As linhas pontilhadas indicam (da esquerda para a direita): os valores de F onde B/R é igual a 50% do seu valor inicial (isto é, F0,5; F0,1); e Fmax tal como foi definido na Caixa 18.
Em todas estas análises, o valor de M é retirado da tabela POPCRESCIMENTO (veja secção sobre Mortalidade Natural), introduzido pelo utilizador, ou gerado a partir das equações empíricas de Pauly (1980), as quais assumem a seguinte forma para o comprimento:
logM = -0.066 - 0.279logL¥ + 0.6543 logK + 0.4634 logT …9)
e para o peso
logM = -0.2107 - 0.0824 logW¥ + 0.6757 logK + 0.4627 logT 10)
onde M e K são expressos numa base anual, L ¥ e W ¥ são expressos em cm (TL) e g (peso fresco) respectivamente, e onde T representa a temperatura média ambiental (água) em °C. [Uma rotina interna converte valores baixos de T (até 2°C) no seu equivalente fisiológico mais alto (Pauly 1980); uma outra rotina converte os valores de L¥, primeiramente expressos como SL ou FL, em TL de modo a que possam ser utilizados na Equação (9); outras medidas de crescimento (WD, OT ou NA) são deixadas inalteradas.]
Os parâmetros W¥ e K são sempre retirados da tabela POPCRESCIMENTO, juntamente com to, quando disponível. Uma rotina permite introduzir valores de Lr e to acima do seu zero (veja Caixa 13). Repare que Lr deverá permanecer metade de L¥.
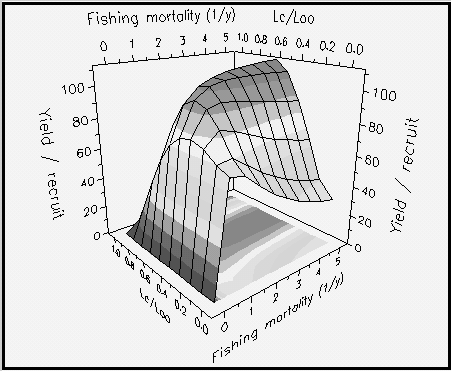
Fig. 26. Curva de iso-rendimento tri-dimensional para Plectropomus leopardus em função do tamanho relativo no início da fase explorada Lc/L ¥ e da mortalidade por pesca. Os parâmetros utilizados são: L ¥ = 45 cm; M/K = 2; tc = 0.12 ano; tmax = 26 anos; e Lc = 20 cm. Notar a pequena variação de Lc/L ¥ " 0,6 para o Y/R máximo e F>1,5 ano -1. Ver Caixa 18 para mais detalhes.
Caso II
As equações (7) e (8) acima descritas assumem que o crescimento em peso é isométrico (i.e. b = 3). Este pressuposto é muitas vezes desajustado da realidade variando geralmente o valor de b, em relações comprimento-peso, entre 2.5 e 3.5 (veja "tabela COMPRIMENTO-PESO", neste volume). Um método possível para lidar com valores de b ¹ 3 é recorrer ao uso da função incompleta b, tal como proposto por Jones (1957).
Caixa 18. Gráficos de rendimento por recruta e biomassa por recruta.
A rotina Y/R incluída na FishBase é construída de modo a que os gráficos Y/R e B/R sejam apresentados mesmo que apenas estejam disponíveis na tabela POPCRESCIMENTO os valores de L¥ e K. Isto é, são fornecidos por defeito para os parâmetros em falta do seguinte modo:
O Caso I (veja Análise de rendimento por recruta, neste volume) aplica-se quando W¥ está disponível e b = 3. O gráfico inicial assume tr = 0, to = 0 (se estes valores não estiverem disponíveis na tabela POPCRESCIMENTO), e Lc = 0.05 × L¥. O valor de M é tratado como no Caso III, excepto na equação (10) que fornece uma estimativa de M. Os parâmetros tr e to podem ser posteriormente alterados, o primeiro introduzindo um valor de Lr (modificado internamente em tr), e o segundo introduzindo um valor escolha, ou uma estimativa aproximada, obtida através da equação
log(-t0) »
-0.3922 - 0.2752 logL¥
- 1.038 logK
onde L¥ está em cm (TL), e K em ano-1, e que é baseada em 153 tripletos de valores de to , L¥ e K seleccionados de Pauly (1978) de modo a cobrir a grande diversidade de taxa e tamanhos dos peixes (Pauly 1979). Na Equação (7) o valor de tmáx é obtido a partir da tabela ESPÉCIES quando está disponível, caso contrário tmáx = ¥ e é utilizada a Equação (8).
O Caso II é utilizado quando W¥ está disponível e b = 3; t
O Caso III aplica-se quando W¥ não está disponível e tem que se utilizar L¥. É assumido que b = 3, to = 0, tmax = ¥ , tr,/sub> = 0, e Lc = 0.05 × L¥. São fornecidas rotinas para entrada de valores de M diferentes do "default", estabelecido para M = 2K (é fornecida uma rotina que utiliza a Equação (9), ou seja, é necessário introduzir T em °C), e vários Lc;
Os gráficos de biomassa/recrutamento apresentados juntamente com a análise Y/R baseiam-se em versões modificadas das Equações (7), (8) e (12) e devem ser tomados em consideração quando se interpretam os gráficos Y/R (ver abaixo).
Os gráficos aparecem em dois modos: (1) 2D, com as formas de Y/R e as linhas B/R dependendo de Lc; e (2) 3D, isto é, como diagramas da produção (biomassa) em isopletas. Os primeiros gráficos mostram três pontos de referência:
Emax ou Fmax , i.e., o valor de E ou F associado com o maior valor possível de Y/R para um dado valor de Lc;
E0.1 e F0.1, o valor de E ou F para o qual o declive de Y/R é 1/10 do seu valor na origem;
E0.5 e F0.5 , os valores de E ou F relacionados com uma redução de biomassa (por recruta) de 50% no stock inexplorado.
Estes pontos de referência, que correspondem às três linhas verticais tracejadas da Fig. 19, são discutidos na parte final da secção "Análise de rendimento por recruta".
Referências
Pauly, D. 1978. A preliminary compilation of fish length growth performance. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy's growth formula. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 63, 156 p.
Daniel Pauly
Aqui, a produção-por-recruta, quando tmáx = ¥, é dada por
![]() …11)
…11)
where X = ![]() ;
;
P = Z/K ;
Q = b + 1 ;
b
= é o símbolo da função imcompleta beta
r1 e r2 são definidos tal como na equação (7).
A rotina Y/R da FishBase verifica automaticamente se b = 3. Se b não for igual a 3 é utilizada a equação (11) (veja Caixa 18). Por outro lado, os parâmetros utilizados são os mesmos do que na equação (8).
Caso III
Quando os parâmetros de uma relação comprimento-peso não estão disponíveis, ainda é possível efectuar uma análise Y/R, utilizando o conceito de rendimento por recruta relativo (Y'/R) de Beverton & Holt (1964) definido por
onde c = Lc/L¥, e a taxa de exploração é definida por E = F/Z.
Repare que a relação entre Y/B e Y/R é dada,
enquanto que a relação entre F e E é dada por
Note também que a escala de E não é linear, com E = 1 correspondendo a F = ¥. Assim, valores elevados de E indicam níveis de esforço insustentáveis, se não praticamente impossíveis.
A utilização de modelos de rendimento por recruta: AVISOS
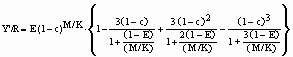 …12)
…12)![]() … 13)
… 13)![]() …14)
…14)
Apesar de ainda adaptados à gestão de certos stocks, os modelos de rendimento por recruta devem ser utilizados com precaução. Os pescadores não estão interessados num rendimento por recruta imaginária mas antes numa produção material de peixe, e esta corresponderá ao rendimento por recruta multiplicado pelo número absoluto de peixes produzidos no stock. O rendimento só é directamente proporcional ao rendimento por por-recruta, para uma grande variação de mortalidades de pesca, se for assumido que não existe relação - para uma ampla gama de valores de F ou E - entre o tamanho do stock parental e a sua descendência (o que não é verdade, veja a tabela "RECRUTAMENTO").
Assim, os valores de F ou de E necessários para produzir um máximo de rendimento por recruta terão tendência a gerar valores de produção extremamente baixos, porque Fmax e Emax reduzem o stock parental a um nível em que são produzidos poucos recrutas. Além disso, deve ser compreendido que a descoberta das análises de rendimento por recruta só se aplicam a situações de equilíbrio a longo prazo. A curto prazo, um aumento da mortalidade de pesca ou uma diminuição no tamanho na captura resulta sempre em produções mais elevadas, mesmo quando a análise prevê valores baixos. Do mesmo modo, uma diminuição na mortalidade de pesca ou um aumento no tamanho da primeira captura resulta sempre em produções mais baixas a curto prazo, apesar de, com o decorrer do tempo, se alcançar produções mais elevadas. A duração do período de transição pode ser de vários anos em peixes com grande longevidade e que estão sujeitos a exploração há muitos anos, tal como o bacalhau. Em peixes com menor longevidade, o período de transição será mais pequeno. No caso dos peixes com período de vida muito curto, a distinção entre efeitos de curto e longo prazo nem se aplica, uma vez que os stocks nunca estão em equilíbrio.
Uma outra importante característica da análise de rendimento por recruta é o facto de esta ser maximizada para valores baixos de E e F, apenas no caso de peixes de grandes dimensões e longevidade, e com fraca mortalidade. Em pequenos peixes tropicais, com valores de M elevados, os valores de E e F que maximizam o rendimento por recruta são normalmente altos. Assim, pode ser muito muito enganadora a gestão de pescas tropicais baseada apenas na análise Y/R para espécies de peixes de pequena dimensão. [Esta nota ignora o bias adicional devido à noção de recrutamento e selecção irregular implicita nas equações (7), (8) e (12); veja Pauly & Soriano 1986, e Silvestre et al. 1991]
Por esta e outras razões, surgiu um acordo (arbitrário) para limitar F ao ponto onde o declive da curva de rendimento por recruta tem 1/10 do seu valor na origem (Gulland & Boerema 1973). Este conceito, denominado F0.1, pode ser visto como um substituto para MEY (Rendimento Económico Máximo), aplicável em situções onde não existem dados sobre o desempenho das pescas. Um conceito análogo ao F0.1, mas aplicável à taxa de exploração E é E0.1, e é utilizado em conjunção com o Caso III descrito acima.
Uma outra precaução nas análises Y/R é a de examinar sempre a curva de biomassa por recruta correspondente (B/R or B'/R), que é calculada juntamente com o rendimento por recruta (obtem-se B/R dividindo Y/R por F, veja, por ex., a equação 8). O ponto de referência apropriado é o valor F (ou E) que reduz B/R (ou B'/R) a metade do seu nível inexplorado (quando F ou E = 0), i.e., ao nível de biomassa que maximiza o rendimento Supérfluo gerando assim MSY (cf. Schaefer 1954, 1957; Gulland 1983; ou Pauly 1984). Este valor é aqui referido como F0.5 ou E0.5.
Clique o botão Biologia na janela ESPÉCIES, o botão Dinâmica de Populações na janela BIOLOGIA, o botão Crescimento na janela DINÂMICA DE POPULAÇÕES e, depois de seleccionar uma análise, o botão Y/R na tabela CRESCIMENTO.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Beverton, R.J.H. and S.J. Holt. 1964. Table of yield functions for fishery management. FAO Fish. Tech. Pap. 38, 49 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic methods. FAO/Wiley, New York.
Gulland, J.A. and L. Boerema. 1973. Scientific advice on catch levels. Fish. Bull. (US) 71:325-335.
Jones, R. 1957. A much simplified version of the fish yield equation. Doc. No. P. 21. Paper presented at the Lisbon joint meeting of International Commission Northwest Atlantic-Fisheries, International Council for the Exploration of the Sea, and Food and Agriculture Organization of the United Nations. 8 p. (Mimeo).
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish population dynamics in tropical waters: a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and M. Soriano. 1986. Some practical extensions to Beverton and Holt's relative yield-per-recruit model, p. 491-495. In J.L. Maclean, L.B. Dizon and L. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries Society, Manila.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 191, 382 p.
Schaefer, M.B. 1954. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries.Inter-Am. Trop. Tuna Comm., Bull. 1(2):27-56.
Schaefer, M.B. 1957. A study of the dynamics of the fishery for yellowfin tuna in the eastern tropical Pacific Ocean. Inter-Am. Trop. Tuna Comm., Bull. 2:247-268.
Silvestre, G., M. Soriano and D. Pauly. 1991. Sigmoid selection and the Beverton and Holt equation. Asian Fish. Sci. 4(1):85-98.
Daniel Pauly e Felimon C. Gayanilo, Jr.