As relações comprimento-peso são importantes em haliêutica, particularmente para inferir as distribuições de frequência nas capturas totais a partir de amostras, ou para estimar a biomassa a partir de observações subaquáticas. Esta tabela fornece os valores a e b de cerca de 4.000 relações comprimento-peso da fórmula W = a. Lb, pertencentes a cerca de 1.700 espécies de peixes.
No entanto, as relações comprimento-peso publicadas são, por vezes, difíceis de utilizar, porque podem-se fundamentar num tipo de comprimento (p.ex., comprimento à furca) diferente do comprimento utilizado para outro fim (p.ex., o comprimento total para o crescimento).
Por consequência, para facilitar a conversão entre diferentes tipos de comprimento, concebemos uma tabela suplementar COMPRIMENTO-COMPRIMENTO, que é apresentada mais abaixo. Contém regressões lineares ou racios reunindo os diferentes tipos de comprimentos (p. ex., LF em função de LT).
Estas relações comprimento-peso foram extraídas de cerca de 1.100 referências, p.ex., Carlander (1969; 1977); Cinco (1982); Dorel (1985); Bohnsack & Harper (1988); Coull et al. (1989); Torres (1991); e Kulbicki et.al.(1993).
Incluímos um campo calculado com o peso dum peixe de 10 cm ( que ser da ordem dos 10 g para um peixe fusiforme "normal") para permitir a detecção de erros grosseiros, sabendo a forma do corpo da espécie. Também existe um botão de gráficos, na tabela do sumário, que quando accionado, mostra plots das relações comprimento-peso que podem ser usados para identificar curvas que se afastam da tendência geral.
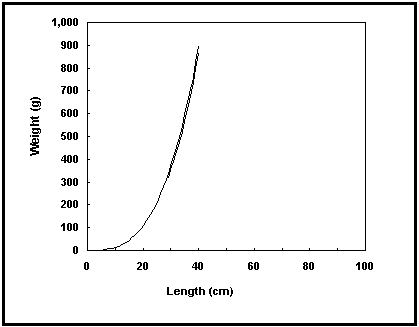
Fig. 15. As duas relações comprimento-peso actualmente disponíveis na FishBase para Lutjanus bohar. Notar que pode usar este gráfico para estimar um peso em função de um dado comprimento.
Um campo de escolha indicando o método de cálculo dos parâmetros a e b, da relação comprimento-peso, foi incluído à tabela; estes métodos são:
Tipo I (ou predictivo) regressão linear de logW sobre logL (método utilizado na maioria dos casos);
Tipo II (ou funcional) regressão linear de logW sobre logL (como sugerido por Ricker 1975, mas raramente usado, visto que as relações comprimento-peso são geralmente usadas para conhecer o W a partir do L);
O mesmo que (1) ou (2), mas corrigindo os bias sugeridos por Sprugel (1983; ver também Vakily et al. 1986);
Regressão não linear de W sobre L, como recomendado por ex., por Saila et al. (1988);
De amostras de frequências de comprimento e os seus pesos totais, usando os algoritmos de Pauly & Gayanilo (1996);
Fazendo b=3, e usando um par de valores L-W para calcular a constante a;
Fazendo b=3, e usando a média geométrica de L e W para obter o a, ou calculando a para cada par de dados, tomando depois a média dos valores resultantes para a;
Qualquer outro método (p. ex., o de Lenarz 1994, como especificado no campo "Comentários").
Clique o botão Biologia na janela ESPÉCIES, o botão Dinâmica da populações na janela BIOLOGIA e o botão Relação L-W na janela DINÂMICA DE POPULAÇÕES. O nome interno desta tabela é POPLW.
Bohnsack, J.A. and D.E. Harper. 1988. Length-weight relationships of selected marine reef fishes from the southeastern United States and the Caribbean. NOAA Tech. Mem. NMFS-SEFC-215, 31 p.
Carlander, K.D. 1969. Handbook of freshwater fishery biology. Vol. 1. The Iowa State University Press, Ames, Iowa. 752 p.
Carlander, K.D. 1977. Handbook of freshwater fishery biology. Vol. 2. The Iowa State University Press, Ames, Iowa. 431 p.
Cinco, E. 1982. Length-weight relationships of fishes, p. 34-37. In D. Pauly and A.N. Mines (eds.) Small-scale fisheries of San Miguel Bay: biology and stock assessment. ICLARM Tech. Rep. 7, 124 p.
Coull, K.A., A.S. Jermyn, A.W. Newton, G.I. Henderson and W.B. Hall. 1989. Lenght-weight relationships for 88 species of fish encountered in the North Atlantic. Scottish Fish. Res. Rep. 43, 80 p.
Dorel, D. 1985. Poissons de l'Atlantique nord-est: relations taille-poids. Institut Français de Recherche pour l'Exploration de la Mer, Paris. 165 p.
Kulbicki, M., G. Mou Tham, P. Thollot and L. Wantiez. 1993. Length-weight relationships of fish from the lagoon of New Caledonia. Naga, the ICLARM Q. 16(2-3):26-29.
Lenarz, W.H. 1994. Estimation of weight-length relationship from group measurements. US Fish Bull. 93:198-202.
Pauly, D. and F.C. Gayanilo, Jr. 1996. Estimating the parameter of length-weight relationship from length-frequency samples and bulk weights, p. 136. In D. Pauly and P. Martosubroto (eds.) Baseline studies of biodiversity: the fish resources of western Indonesia. ICLARM Stud. Rev. 23, 321 p.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. B. Can. 191, 382 p.
Saila, S.B., C.W. Recksiek and M.H. Prager. 1988. Basic fishery science programs: a compendium of microcomputer programs and manual of operation. Elsevier Science Publishing Co., New York. 230 p.
Sprugel, D.G. 1983. Correcting for bias in log-transformed allometric equations. Ecology 64(1):209-210.
Torres, F. Jr. 1991. Tabular data on marine fishes from Southern Africa, Part I. Length-weight relationships. Fishbyte 9(1):50-53.
Vakily, J.M., M.L. Palomares and D. Pauly. 1986. Computer programs for fish stock assessment: applications for the HP41 CV calculator. FAO Fish. Tech. Pap. 101 Suppl. 1, 255 p. Rome.