Que o crescimento dos peixes apresenta oscilações sazonais é um facto já relatado pelos pioneiros da biologia pesqueira, particularmente de T.W. Fulton (1901, 1904) que inventou com C. G. J. Petersen, a análise de frequências de comprimento. Este conhecimento passou entretanto ao segundo plano assim que os cientistas abandonaram gradualmente esta análise (em favor do estudo dos anéis de crescimento nos otólitos, escamas e ossos) no cálculo das taxas de crescimento e no traçado das respectivas curvas (Went 1972). Assim, na sua obra clássica de 1952, Beverton & Holt não trataram as oscilações sazonais senão como mera curiosidade académica, e em particular, não encontraram nenhuma razão para modificar a equação da curva de von Bertalanffy (CVB) para ter em conta essas oscilações, que se verificavam em todos os peixes que estudaram.
Depois que von Bertalanffy e Müller evocaram o crescimento sazonal em 1943, Ursin foi o primeiro a publicar uma CVB que tem em conta estas oscilações (1963a, 1963b). Outras modificações foram de seguida propostas (Pitcher & McDonald 1973; Daget & Ecoutin 1976), depressa seguidos por uma sucessão de melhoramentos dos modelos (Cloern & Nicols 1978; Pauly & Gaschütz 1979; Appeldoorn 1987; Somer 1988; Soriano & Pauly 1989). Os exemplos de aplicação apresentados por estes autores puseram claramente em evidência que os modelos de crescimento que não considerassem explicitamente as oscilações sazonais omitiriam um aspecto essencial no processo de crescimento (Pauly 1990, 1994).
E mais, mesmo nos trópicos, a pequena diferença de dois graus entre o inverno e o verão é suficiente para induzir oscilações sazonais de crescimento que são estatisticamente significativas embora visualmente não detectáveis (Pauly & Ingles 1981; Longhurst & Pauly 1987).
O modelo de crescimento que melhor toma em linha de conta as oscilações sazonais é o de Somer (1988), cuja expressão é:
Lt = L¥ {1 – exp – [ K (t – t0) + S(t) – S(t0)]} …1)
onde
L¥ , K and t0 se definen como en la CVB estándar se definen como en la CVB estándar;
S(t) = (CK/2p ) Sin p (t – t
s); and
S(t0) = (CK/2p ) Sin p (t0 - t
s).
A equação (1) tem dois parâmetros a mais que a CVB standard: C e ts. C exprime a amplitude das oscilações de crescimento e é o mais fácil de interpretar. Quando C=0, a equação (1) toran-se na CVB standard; quando C=0,5, as oscilações sazonais são tais que o crescimento é aumentado 50% no momento do pico de crescimento do Verão, e rapidamente, reduzido em 50% no Inverno. Quando C=1, o crescimento varia de 100%, que dizer, dobra no Verão e é nulo no Inverno (ver fig. 21).
O segundo parâmetro novo, ts, corresponde à duração entre t=0 e o começo duma oscilação sinusoidal de crescimento. Para ser representada, é necessário definir um "ponto invernal) WP=ts+0,5 que exprime o período do ano em que o crescimento é mais lento. WP é frequentemente próximo de 0,1 no hemisfério norte (quer dizer, meados de Fevereiro) e de 0,6 no hemisfério sul (meados de Agosto), donde o seu nome. [Note que a alternância das temperaturas estivais altas e invernais baixas não é necessáriamente a causa das oscilações sazonais do crescimento; nos peixes dulçaquícolas do Amazonas, p. ex., estas oscilações são devidas à alternância das estações das chuvas e de seca. Note também que a equação (1) não pode descrever longos períodos de crescimento nulo (nem utilizar valores de C>1), problema discutido por Pauly et al. 1992)]. Como este modelo e os seus predecessores (particularmente, o modelo de Pauly & Gaschütz 1979) foram adaptados a numerosos dados de oscilações sazonais de crescimento, estão disponíveis avaliações de C para uma vasta gama de espécies e de habitats.
A tabela POPGROWTH inclui a maioria da avaliações de C publicadas para os peixes, combinadas com avaliações das diferenças de temperatura verão-inverno (DT; diferença dos valores mensais médios, em ºC). Como pode ser constatado na Fig. 22, estes valores de C aumentam com DT, para um valor de C próximo de 1, quando DT é cerca de 10ºC.
Algumas implicações fisiológicas desta relação são conhecidas desde o princípio dos anos 80 (ver, p. ex., Pauly & Ingles 1981), e são discutidas por Longhurst & Pauly (1987).
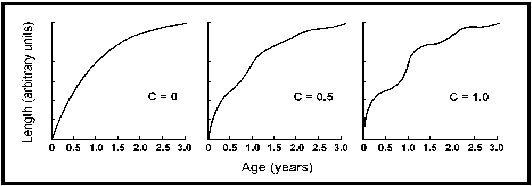
Fig. 21. Efeito do parâmetro de amplitude C sobre uma curva de von Bertalanffy com L ¥ =25 unidades, K=1 anos -1, t0 =0 e ts=0.
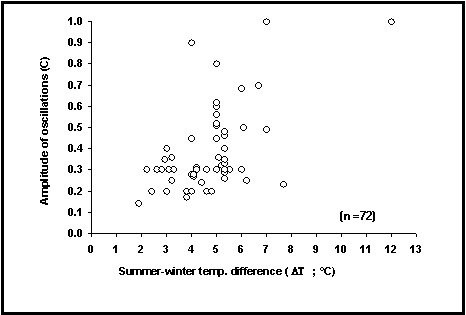
Fig.22. Relações entre o parâmetro C e as diferenças de temperatura Verão-Inverno do seu habitat (DT em ºC) para 72 populações de peixes. C reflete a amplitude das oscilações sazonais de crescimento.
Para aceder ao gráfico da figura 22, clicar sobre o botão Relatórios na janela MENÚ PRINCIPAL, depois sobre o botão Gráficos na janela RELATÓRIOS PRÉ-DEFINIDOS, depois no botão Dinâmica das populações na janela GRÁFICOS, e finalmente sobre o botão Crescimento sazonal na janela DINÂMICA DAS POPULAÇÕES.
Appeldoorn, R. 1987. Modifications of a seasonal growth function for use with mark-recapture data. J. Cons, CIEM 43: 194-198.
Bertalanffy, L. von e I. Müller. 1943. Untersuchungen über die Gesetzlichkeit des Wachstums. VIII. Die Rev. Biol. 35: 48-95.
Beverton, R. J. H. e S. J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol.19, 533p.
Cloern, J.E. e F.H. Nicols. 1978. A von Bertalanffy growth model with a seasonally varying coefficient. J. Fish. Res. Board Can. 35: 1479-1482.
Daget, J. e J. M. Ecoutin. 1976. Modéles mathématiques de production applicables aux poissons tropicaux subissant un arrêt annuel prolongué de croissance. Cah. ORSTOM, sér. Hydrobiol. 10(2): 59-69.
Fulton, T. W. 1901. The rate of growth of the cod, haddock, whiting and Norway pout. 19th Ann. Rep. Fish. Board Scotland. Part III: 154-228.
Fulton, T. W. 1904. The rate of growth of fishes. 22th Ann. Rep. Fish. Board Scotland. Part III: 141-240.
Longhurst, A. e D. Pauly. 1987. Ecology of tropical oceans. Academic Press, San Diego, California. 407p.
Pauly, D. 1990. Length-converted catch curves and the seasonal growth of fishes. Fishbyte 8(3):33-38.
Pauly, D. 1994. Length-converted catch curves and the seasonal growth of fishes. Fishbyte 8(3):24-29.
Pauly, D. e G. Gaschütz. 1979. A simple metod for fitting oscillating length growth data, with a program for pocket calculators. ICES. CM 1979/6: 24. Demersal Fish Committee, 26p.
Pauly, D. e J. Ingles. 1981. Aspects of the growth and natural mortality of exploited coral reef fishes, p. 89-98. In E.D. Gomez, C.E. Birkeland, R.W. Buddemeyer, R.E. Johannes, J.A. Marsh et R.T. Tsuda (éds.). Proceedings of the Fourth International Coral Reef Symposium. Vol. 1, Marine Science Center, University of the Philippines, Quezon City.
Pauly, D., M. Soriano-Bartz, J. Moreau e A. Jarre. 1992. A new model accounting for seasonal cessation of growth in fishes. Aust. J. Mar. Freshw. Res. 43 : 1151-1156.
Pitcher, T.J. e P.D.M. MacDonald. 1973. Two models for seasonal growth in fishes. J. Appl. Ecol. 10 : 599-606.
Somer, I.F. 1988. On a seasonally oscillating growth function. Fishbyte 6(1) : 8-11.
Soriano, M. e D. Pauly. 1989. A method for estimating the parameters of a seasonally oscillating growth curve from growth increments data. Fishbyte 7(1) : 18-21.
Ursin, E. 1963a. On the incorporation of temperature in the von Bertalanffy growth equation. Medd. Danm. Fisk. Havunders. N.S. 4(1) : 1-16.
Ursin, E. 1963b. On the seasonal variation of growth rate and growth parameters in Norway pout (Gadus esmarki) in Skagerrak. Medd. Danm. Fisk. Havunders. N.S. 4(2) : 17-29.
Went, A.E.J. 1972. Seventy years agrowing : a history of the International Council for the Exploration of the Sea, 1902-1972. Rapp. P.-v Réun. CIEM 165. 252 p.
Daniel Pauly