Em haliêutica, a mortalidade é usualmente expressa sob a forma de taxas instantâneas, assim:
![]() …1)
…1)
onde N0 e N1 são os números sucessivos duma população afectada pela taxa de mortalidade (total) Z, durante o intervalo de tempo Dt.
Sumariamente temos:
Z = F + M ...2)
onde F é a mortalidade por pesca e M é a mortalidade natural, causada por qualquer outro factor que não a pesca (num stock não explorado Z=M, obviamente).
Estimativas de mortalidade natural são difíceis de obter (excepto em populações não exploradas, que tendem a ser inacessíveis para o estudo, e são cada vez mais raras). Assim, toda a estimativa de M bem documentada na literatura foi incorporada na tabela POPCRESCIMENTO, que inclui agora mais de 400 estimativas de mortalidade natural, de mais de 200 espécies (ver Caixa 12). Cerca de 42% destas estimativas são de Pauly (1980; veja "Análise da Produção-por-recruta") enquanto que 21% são de Beverton & Holt (1959) e de Djabali et al. (1993) .
Os dados de mortalidade natural da FishBase são baseados naquela que é seguramente a maior compilação de estimativas de mortalidade natural em todo o mundo, isto é, não existem dados similares que possam ser utilizados para verificar as generalizações obtidas a partir desta série de dados. Deste modo, uma vez que é difícil obter replicação independente dos nossos resultados, deveremos ser cuidadosos na apresentação de generalizações baseadas nesta série de dados.Assim, limitámo-nos a apresentar dois gráficos que confirmam generalizações anteriores de Beverton & Holt (1959) e Pauly (1980). O primeiro destes gráficos (Fig. 17) é um gráfico do logM vs logK, os parâmetros da equação de crescimento de von Bertalanffy. Confirma-se que K, que está relacionado com a longevidade, é um bom indicador de M. No entanto, a variância é elevada o que sugere que também outros factores podem influenciar M.
O segundo gráfico (Fig. 18) representa dois dos factores que influenciam M: tamanho e temperatura ambiental. Os pontos são estimativas de logM vs estimativas correspondentes logL¥; os pontos a preto representam as estimativas para temperaturas acima de 17°C (cerca de 50% de todos os casos) e os pontos brancos para as restantes.
Como é possível ver no gráfico, M está não só relacionado com L¥ (e com K; veja Fig. 17), mas também com a temperatura.
Referências
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O'Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol 5, J. & A. Churchill Ltd., London
Charnov, E. 1993. Life-history invariants: some explorations of symmetry in evolutionary ecology. Ecology and Evolution. Oxford University Press, Oxford. 128 p.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly
É de notar que estes resultados são independentes, isto é não foram calculados usando modelos empíricos, ligando valores de M a variáveis incorrectas, como é explicado por Pauly (1980). Assim, as estimativas de M apresentadas, podem ser utilizadas para construir novos modelos empíricos.
Como ajuda, a temperatura média ambiental (em 0C) foi adicionada ao registo POPCRESCIMENTO que inclui a estimativa M. Também o método de cálculo de M está registado, como uma das seguintes escolhas: curva de capturas num stock não explorado; comprimento médio dos indivíduos do stock não explorado; marcação-recaptura; "plot" de Z no esforço de pesca; "plot" parabólico de Z na captura; Ecopath modelo trófico (Christensen & Pauly 1993); outro método.
Estas técnicas são descritas nos livros de texto indicados na tabela POPCRESCIMENTO, com excepção das envolvidas no modelo Ecopath, descrito na Caixa 14.
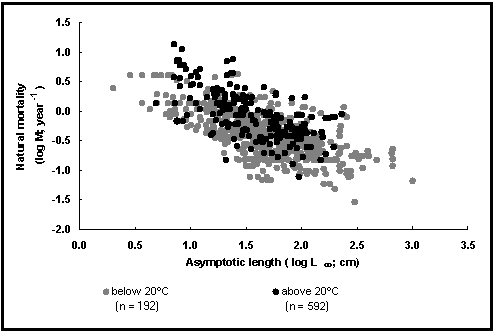
Fig. 24. Mortalidade natural em função do comprimento assimptótico para os peixes tropicais (círculos negros) e os outros peixes (círculos claros). Notar o efeito da temperatura. Consulte a caixa 17 para mais detalhes.
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in nature and their relation to growth and other physiological characteristics, p. 142-180. In G.E.W. Wolstenholme and M. O'Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of animals. Vol. 5, J. & A. Churchill Ltd., London.
Christensen, V. and D. Pauly, Editors. 1993. Trophic models of aquatic ecosystems. ICLARM Conf. Proc. 26, 390 p.
Djabali, F., A. Mehailia, M. Koudil and B. Brahmi. 1993. Empirical equations for the estimation of natural mortality in Mediterranean teleosts. Naga, ICLARM Q. 16(1):35-37.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel Pauly e Crispina Binohlan