Durante o processo de crescimento dos peixes, existem alterações no tamanho (peso ou comprimento) ao longo do tempo e quaquer tentativa de representação ou comparação de crescimentos deve considerar ambas as dimensões. No entanto, a comparação de curvas de crescimento que relacionam tamanho e tempo não é directa. Com efeito, dependendo da definição de crescimento "rápido" ou "lento" é possível entrar em contradição quando duas curvas se cruzam. Deste modo, Kinne (1960) escreveu que a taxa de crescimento observada em peixes juvenis não se mantém ao longo da vida. Peixes de crescimento inicial lento podem ultrapassar peixes de crescimento inicial rápido e alcançar um maior comprimento na fase adulta." (Este fenómeno é bem ilustrado na Fig. 17).
Na FishBase são utilizados os parâmentos da função de crescimento de von Bertalanffy ou CVB (von Bertalanffy Growth Function) (veja a "tabela POPCRESCIMENTO", neste volume) para descrever o crescimento dos peixes. Contudo, isto não resolve por si só o problema mencionado por Kinne (1960) uma vez que nenhum destes parâmentros possui a unidade do crescimento (i.e., comprimento vs tempo ou peso vs tempo). L¥ e W¥ representam apenas o tamanho, e K e to têm apenas a dimensão tempo-1 e tempo, respectivamente. No entanto, várias combinações destes parâmentros, e.g., L¥. K, possuem uma dimensão adequada (l/t) da taxa de crescimento (Gallucci & Quinn 1979). Apesar da base logarítmica os índices de crescimento:
Ø
’ = logK + 2logL¥ …1)e
Ø
têm a unidade correcta da taxa de crescimento e são amplamente utilizados para comparar o crescimento de diversos peixes e invertebrados, devido a estes terem uma distribuição normal para diferentes populações de uma mesma espécie (veja, por ex., Moreau et al. 1986). Esta última característica também permite estimar K a partir de L¥ ou W¥ quando a o seu Ø' ou Ø (média) é conhecido a partir de uma ou mais populações (Munro & Pauly 1983; Pauly & Munro 1984).
Os declives de 2 e 2/3 nas equações (1) e (2) respectivamente, foram estimados por Pauly (1979) a partir de uma grande série de dados documentados em Pauly (1978, 1979), e que são agora incluídos na FishBase. A equação (1) implica que que os gráficos de logK vs logL¥ tenham em média um declive igual a -2. Do mesmo modo, a equação (2) implica que os gráficos de logK vs logL¥ tenham em média um declive de -2/3.
Uma "nuvem" auxiométrica (do grego "crescimento" e "medida") é um gráfico do parâmentro K de CVB vs tamanho assimptótico (L¥ or W¥), com ambos os eixos em escala logarítmica. Uma população com uma série de parâmentros de crescimento (L¥, K or W¥ , K) é representada por um único ponto, e diferentes populações da mesma espécie terão tendência a formar um grupo ("cluster") de pontos. Uma vez que as equações (1) e (2) implicam que a estes grupos de pontos possam ser ajustadas linhas de regressão de declive conhecido, também aos grupos de pontos podem ser sobrepostas elipses com eixos de declive 2 ou 2/3, respectivamente, com intercepções iguais a Ø' ou Ø, e áreas de superfície relacionadas com a variabilidade dos dados representados.
Assim, elipses cuja superfície contém 95% do limite de confiança (S95) de um grupo de pares L¥-K (ou W¥-K), podem ser rapidamente estimadas. Foi desenvolvido um software (AUXIM), descrito em Pauly et al. (1996), para calcular os S95 de grupos com pelo menos 4 pares de valores de L¥ - K ou W¥ - K e que dispõe de rotinas associadas.
Como é aborrecido utilizar o AUXIM como aplicação única, foram incluídas na FishBase 99 sub-rotinas de modo a permitir a análise dos diversos parâmetros de crescimento que este programa contém. Contudo, para a comparação entre peixes de formas bastante diferentes, apenas estão incluídas as rotinas relativas ao crescimento em peso (e Ø, mas não Ø'). Só os peixes "selvagens" podem ser incluídos nas análises (a razão é dada na Caixa 15).
As análises auxiométricas são chamadas a partir da janela RELATÓRIOS, depois de ter identificado um grupo de espécies (pelo ambiente ou por taxon supra-específico, ordem, família ou género). Uma análise auxiométrica compreende:
a representação dum gráfico onde são traçadas todas as elipses para a espécie selecionada tendo pelo menos 4 dados (veja a Fig. 19; Caixa 16) e os valores médios de K e W¥;
a estimativa das distâncias e sobreposições entre espécies (para um minimo de 4 espécies) e a sua representação numa tabela; e
utilização das distâncias de (b) e do algorítmo de agrupamento de McCammon & Wenninger (1970) para construir um dendrograma das distâncias no "espaço crescimento" , ou seja, mostrando as similaridades das espécies selecionadas (Fig. 19).
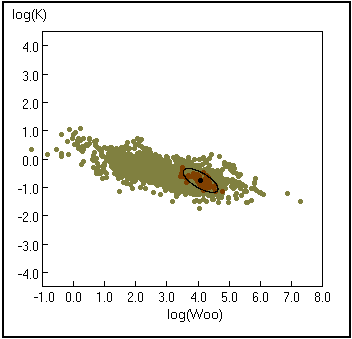
Fig. 19. Curva de K em função de W¥ . Os pontos claros representam todas as espécies para as quais W¥ se encontra disponível na FishBase, os pontos escuros representam as entradas para Gadus morhua. A elipse com um ponto preto no centro representa os limites de confiança de 95%. Consulte a Caixa 16 para os detalhes.
Até ao momento, estas análises têm sido apenas efectuadas para tilápias, Família Cichlidae (Pauly et al. 1996) e peixes da Família Lutjanidae (Pauly & Binohlan 1996), e o seu potencial ainda não foi totalmente explorado. No entanto, cremos que estas análises aumentarão consideravelmente o nosso conhecimento acerca do crescimento e da biologia dos peixes em geral. Gostaríamos de saber a sua opinião a este respeito.
Esta caixa resume as principais características do abordagem utilizada no AUXIM para representar as elipses, tendo a primeira parte deste texto sido adaptada de Pauly et al. (1996). Dado o peso CVB e a definição de Ø, temos
que é a equação do eixo principal da elipse, em que Ø corresponde à intercepção na ordenada.
Ao mesmo tempo, e uma vez que é perpendicular, a equação do eixo menor da elipse é
onde Yo é a ordenada na origem O ponto de intercepção do eixo menor com a abcissa é
Se uma elipse corresponde a uma nuvem de pontos com um limite de confiança de 95%, o comprimento (2 · a) do eixo principal deve estar relacionado com o desvio padrão de X°. Simultaneamente, o comprimento do eixo menor (2 · b) deverá estar relacionado com o desvio padrão de Ø, ou
onde o valor do teste-t se encontra relacionado com o número de pontos (n), com t = 1.96 quando n = ¥ (Sokal & Rohlf 1995); e onde o factor 3/2 · (1/ ((1 + (3/2)2)1/2) entra em consideração com o facto de os eixos da elipse não serem paralelos aos eixos do sistema de coordenadas.
Quando as elipses se referem aos desvios padrão da média dos valores de logW¥ e logK, sd(Xo) e sd(Ø) são substituídas pelos erros-padrão, ou seja, por se(Xo) e se(Ø), respectivamente.
Como utilizar o AUXIM:
A interface do utilizador do AUXIM tem quatro partes:
Botões de comando no canto superior esquerdo do ecrã com funções para: (i) aumentar ou diminuir o tamanho do gráfico auxiométrico (i.e. zoom-in e zoom-out); (ii) abrir a lista de espécies seleccionadas antes de activar a rotina do AUXIM (clicar sobre o botão Relatórios na janela MENÚ PRINCIPAL, depois sobre o botão Gráficos, sobre o botão Dinâmica das Populações, e finalmente, sobre o botão Análises Auxiométricas);
Display das espécies seleccionadas e dos botões de comando que permitem movimentar na lista (canto superior direito);
Display tab, mostrando o gráfico auxiométrico e que também permite visualizar a tabela de distância e sobreposição, tal como o dendograma; e
Sistema de botões de comando para: (i) seleccionar ou cancelar a seleecção de uma espécie da lista; (ii) imprimir o ecrã ou gravar a informação num ficheiro; (iii) abrir o ficheiro ajuda; ou (iv) fechar e regressar à FishBase.
Repare que as funções associadas aos botões de comando, também podem ser efectuadas clicando no botão direito do rato. Também pode seleccionar as espécies clicando duas vezes na espécie e cancelar a selecção carregando na
Pauly, D., J. Moreau and F. Gayanilo, Jr. 1996. A new method for comparing the growth performance of fishes, applied to wild and farmed tilapias, p. 433-441. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (eds.) The Third International Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Sokal, R.R. and F.J. Rohlf. 1995. Biometry. Third edition. W.H. Freeman and Company, San Francisco. 887 p.
Daniel Pauly e Felimon C. Gayanilo, Jr.
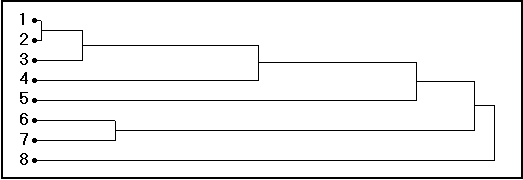
Fig. 20. Dendrograma AUXIM da similaridade (eixo-X em unidades arbitrárias) no "espaço crescimento" definido pelo AUXIM para os Gadidae, com 1= Theragra chalcogramma; 2 = Trisopterus luscus; 3 = Merlangius merlangus; 4 = Micromesistius poutassou; 5 = Melanogrammus aeglefinus; 6 = Gadus morhua; 7 = Pollachius virens; 8= Trisopterus minutus. Como se constata, Theragra chalcogramma e Trisopterus luscus dum lado e Gadus morhua e Pollachius virens do outro, formam dois grupos bem separados, as outras espécies aglomeram-se sucessivamente.
Gallucci, V.F. e T.J. Quinn, II. 1979. Reparameterizing, fitting, and testing a simple growth model. Trans. Am. Fish. Soc. 108(1):14-25.
Kinne, O. 1960. Growth, food intake, and food consumption in an europlastic fish exposed to different temperatures and salinities. Physiol. Zool. 33:288-317.
McCammon, R.B. e G. Wenninger. 1970. The dendrograph. Computer Contribution 48. State Geological Survey. The University of Kansas, Lawrence. 26 p.
Moreau, J., C. Bambino e D. Pauly. 1986. A comparison of four indices of overall fish growth performance, based on 100 tilapia populations (Fam. Cichlidae), p. 201-206. In J.L. Maclean, L.B. Dizon and L.V. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries Society, Manila, Philippines.
Munro, J.L. e D. Pauly. 1983. A simple method for comparing the growth of fishes and invertebrates. Fishbyte 1(1):5-6.
Pauly, D. 1978. A preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy's growth formula. Ber. Inst. Meereskd. Christian-Albrechts-Univ. Kiel 63, 156 p.
Pauly, D. e J.L. Munro. 1984. Once more on the comparison of growth in fish and invertebrates. Fishbyte 2(1):21.
Pauly, D. e C. Binohlan. 1996. FishBase and AUXIM as tools for comparing the life-history patterns, growth and natural mortality of fish: applications to snappers and groupers, p. 223-247. In F. Arreguin-Sánchez, J.L. Munro, M.C. Balgos and D. Pauly (eds.) Biology, fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. 48.
Pauly, D., J. Moreau e F. Gayanilo, Jr. 1996. A new method for comparing the growth performance of fishes, applied to wild and farmed tilapias, p. 433-441. In R.S.V. Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (eds.) The Third International Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Daniel Pauly, Jacques Moreau e Felimon C. Gayanilo, Jr.