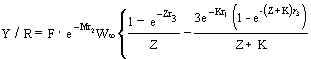Dinâmica das populações
Os parâmetros de crescimento são difíceis de obter
Informação sobre
o tamanho máximo e idade dos peixes, as relações comprimento/peso bem como o
conhecimento dos seus parâmetros de crescimento e da sua mortalidade natural, são
cruciais para uma correcta gestão das pescas.
Embora
estes parâmetros sejam fáceis de obter para a maioria das espécies, tê-los
disponíveis- no formato apropriado- sempre que necessário, é bastante mais
difícil.
Este
problema é ampliado no caso dos parâmetros de crescimento, que são os de mais
difícil obtenção porque, geralmente, provêm de teses de mestrado, ou de
pequenos artigos científicos. Assim, a investigação no campo da avaliação de
stocks pode ser acelerada tornando disponível os parâmetros já conhecidos, quer
para corrigir resultados que foram obtidos utilizando os valores de stocks
vizinhos, quer fornecer dados para a verificação de resultados. O mesmo se
aplica para a mortalidade natural.
Estes
pontos são tão importantes na investigação das pescas tropicais que, em 1987,
foram a razão da proposta de criação duma base de dados que veio a ser a
FishBase, e a qual incluía “um sumário sobre toda a informação de crescimento e
mortalidade de cada espécie [...] com o objectivo último de cobrir 2.500 espécies”
(Pauly 1988).
Incluímos os parâmetros de crescimento de mais de 1.150 espécies
Esta visão
subestimou o número de espécies a incluir na FishBase (que foi 10 vezes
superior ao inicialmente previsto), mas sobreestimou o número de espécies para
as quais existia informação: neste momento, identificámos bibliografia
publicada para mais de 1.150 espécies, e parece-nos que não vai ser possível
chegar às 2.000 espécies até ao ano 2000. No entanto as espécies incluídas
presentemente, representam 95% das espécies comerciais conhecidas, assegurando,
portanto, a relevância das entradas nas três tabelas apresentadas abaixo.
De igual modo, os stocks para os quais são incluídas
mais de 500 séries temporais de recrutamento, pertencem aos stocks de espécies
mais importantes a nível mundial.
Tomámos
algumas precauções no sentido de assegurar uma maior confiança nas entradas das
tabelas, incluindo, de entre outras, a rejeição de resultados não coincidentes
com outros já obtidos para a mesma espécie (ou similar). Contudo, temos
consciência que estas precauções não corrigem erros que sejam originários de
artigos publicados ou da introdução incorrecta dos dados. Esperamos que nos
contactem aquando da detecção de erros deste tipo ou inconsistências, para que possam
ser corrigidos na próxima versão. Vamos confirmar, em especial, os casos
assinalados como “fora da área” no
campo Notas, que se referem a
estudos conduzidos em locais fora da área usual duma dada espécie e que
portanto, se devem, provavelmente, a identificações incorrectas.
A informação sobre a dinâmica das populações pode ser
impressa:
·
por família, usando os
relatórios predefinidos que podem ser acedidos através do Menu Principal da
FishBase;
·
por espécies, a partir
das respectivas tabelas;
·
como parte da sinopse
da espécie.
Referências Pauly, D.
1988. Resource assessment and management program, p. 47-66. In ICLARM
five-year plan (1988-1992), part 1. Directions and opportunities.
International Center for Living Aquatic Resources Management (ICLARM), Manila.
Daniel
Pauly e Crispina Binohlan
A nossa resposta ao
livro Guiness de Recordes Mundiais
A Tabela POPGRÁFICOS
Esta tabela inscreve informação sobre o comprimento
máximo (Lmax), peso (Wmax) e idade (tmax) da espécie considerada, em vários locais onde ocorre. Os maiores valores desta tabela
também se encontram na tabela ESPÉCIES. A tabela POPGRÁFICOS também indica se
os valores Lmax, Wmax e tmax ou as suas várias combinações se referem ao mesmo
indivíduo.
Caixa 10.
Distribuição dos comprimentos máximos pelas espécies de peixes.
Não
é tão simples como parece fazer e interpretar histogramas da frequência das
espécies em relação ao seu comprimento máximo. Assim, para serem
interpretáveis, os histogramas deverão ter classes de tamanho constantes (neste
caso de comprimento), e o número destas classes não deverá ser demasiadamente
baixo nem elevado (i.e., 15-30, veja Sokal and Rohlf 1995). No entanto, o
tamanho máximo dos peixes varia entre 1cm (por ex. góbios) e 14m
(tubarão-baleia Rhincodon typus) e se
fossem utilizadas classes de tamanhos de, por exemplo 50cm (o que originaria um
número apropriado de classes), a maioria das espécies ficaria incluída nas
classes de tamanho mais pequeno e muitas outras classes ficariam vazias.
Utilizando
logarítmos (do comprimento) obtem-se um gráfico (Fig. 11) muito mais
interessante no qual aparecem distribuições normais do log (número de espécies)
vs log (comprimento). Estas linhas
caracterizam os peixes em geral (curva superior em que a maior parte das espécies
de peixes atingem o comprimento máximo de 25 cm) ou algum grupo de interesse
particular (curva a bold).
Nunca
vimos gráficos deste tipo anteriormente e gostariamos de saber a sua opinião
sobre a sua leitura e aplicações possíveis.
Referências
Sokal, R.R. and F.J. Rohlf. 1995. Biometry. Third
edition.W.E. Freeman, San Francisco. 887 p.
Daniel Pauly
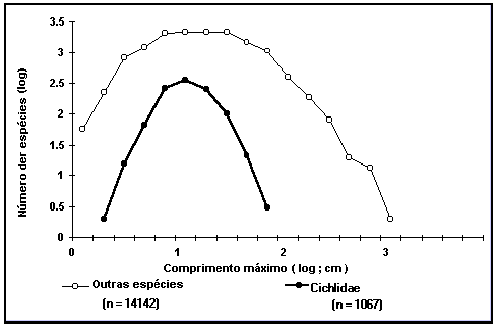
Fig. 11.
Distribuição dos comprimentos da família Cihlidae e das restantes espécies de
peixes da FishBase.
A tabela
contém cerca de 1.200 registos de mais de 700 espécies tiradas de cerca de 400
referências.
Os
utilizadores da FishBase podem considerar esta tabela como a nossa resposta ao Livro Guiness dos Recordes
Mundiais (Anon. 1991) ou pensar sobre os inúmeras maneiras de utilizar estes
dados, p.ex., testar hipóteses sobre teorias biológicas (ver caixa 10).
Como chegar lá Clique
o botão Dinâmica de populações na
janela BIOLOGIA e o botão Tamanhos Máx.
na janela DINÂMICA DE POPULAÇÕES.
Referências Anon. 1991. Das neue Guinness Buch der Rekorde 1992.
Verlag Ullstein, Frankfurt. 354 p.
Crispina Binohlan e Daniel Pauly
Esta
tabela fornece os valores a e b de cerca de 3500 relações comprimento-peso da fórmula A=a ÿ Lb, pertencentes a cerca de 1.500 espécies de peixes.
Esta informação pode ser usada entre outras coisas para calcular a biomassa a
partir de observações subaquáticas das distribuições dos comprimentos.
Fontes Estas
relações comprimento-peso foram obtidas a partir de cerca de 1.100 referências,
p.ex., Carlander (1969; 1977); Cinco (1982); Dorel (1985); Bohnsack and Harper
(1988); Coull et al. (1989); Torres
(1991); e Kulbicki et.al.(1993).
Campos Incluímos
um campo calculado com o peso dum peixe de 10 cm para permitir a detecção de
erros grosseiros, sabendo da forma do corpo da espécie. Também existe um botão
de gráficos, na tabela do sumário, que quando accionado, mostra plots das
relações comprimento-peso que podem ser usados para identificar curvas que se
afastam da tendência normal.
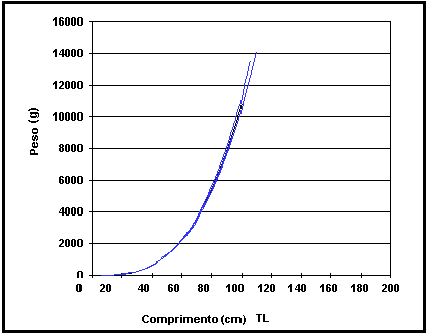
Fig. 12. As
duas relações comprimento-peso existentes na FishBase para a espécie Gadus morhua.
Repare que
também pode utilizar o gráfico para estimar um peso a partir de um determinado
comprimento.
Um
campo de escolha indicando o método de cálculo dos parâmetros a e b, da relação comprimento-peso, foi incluído à tabela; estes
métodos são:
·
Tipo I (ou
predictivo) regressão linear de logW
sobre logL (método utilizado na
maioria dos casos);
·
Tipo II
(ou funcional) regressão linear de logw
sobre logL (como sugerido por Ricker
1975, mas raramente usado, visto que as relações comprimento-peso são
geralmente usadas para conhecer o W
a partir do L);
·
O mesmo que (1) ou (2),
mas corrigindo os bias sugeridos por
Sprugel (1983; ver também Vakily et al.
1986);
Vários métodos podem
ser usados para calcular o peso a partir do comprimento
·
Regressão não linear de
W sobre L, como recomendado por ex., por Saila et al. (1988);
·
De amostras de frequências
de comprimento e os seus pesos totais, usando os algoritmos de Pauly e Gayanilo
(1996);
·
Fazendo b=3, e usando um par de valores L-W para calcular a;
·
Fazendo b=3, e usando a média geométrica de L e W para obter o a, ou
calculando a para cada par de dados,
tomando depois a média dos valores resultantes para a;
·
Qualquer outro método
(a especificar no campo “Comentários”).
Como chegar lá Clique o botão Biologia
na janela ESPÉCIES, o botão Dinâmica da
populações na janela BIOLOGIA e o botão Relação L-W na janela DINÂMICA DE POPULAÇÕES.
Referências Anon. 1991.
Das neue Guinness Buch der Rekorde 1992. Verlag Ullstein, Frankfurt. 354 p.
Bohnsack, J.A. and D.E. Harper. 1988. Length-weight relationships of selected
marine reef fishes from the southeastern United States and the Caribbean. NOAA
Tech. Mem. NMFS-SEFC-215, 31 p.
Carlander, K.D. 1969. Handbook of freshwater fishery biology.
Vol. 1. The Iowa State University Press, Ames, Iowa. 752 p.
Carlander, K.D. 1977. Handbook of freshwater fishery biology.
Vol. 2. The Iowa State University Press, Ames, Iowa. 431 p.
Cinco, E. 1982. Length-weight relationships of fishes, p.
34-37. In D. Pauly and A.N. Mines (eds.) Small-scale fisheries of San Miguel Bay: biology and stock assessment. ICLARM Tech. Rep. 7, 124 p.
Coull, K.A., A.S. Jermyn, A.W. Newton, G.I. Henderson and W.B. Hall. 1989. Lenght-weight relationships for 88 species of
fish encountered in the North Atlantic. Scottish Fish. Res. Rep. 43, 80 p.
Dorel, D. 1985. Poissons de l'Atlantique nord-est:
relations taille-poids. Institut Français de Recherche pour l'Exploration de la
Mer, Paris. 165 p.
Kulbicki, M., G. Mou Tham, P. Thollot and L.
Wantiez. 1993. Length-weight relationships of fish from the
lagoon of New Caledonia. Naga, the ICLARM Q. 16(2-3):26-29.
Lenarz, W.H. 1994. Estimation of weight-length relationship
from group measurements. US Fish Bull. 93:198-202.
Pauly, D. and F.C. Gayanilo, Jr. 1996. Estimating the parameter of length-weight
relationship from length-frequency samples and bulk weights, p. 136. In D. Pauly and P. Martosubroto (eds.)
Baseline studies of biodiversity: the fish resources of western Indonesia.
ICLARM Stud. Rev. 23, 321 p.
Ricker, W.E. 1975. Computation and interpretation of
biological statistics of fish populations. Bull. Fish. Res. B. Can. 191, 382 p.
Saila, S.B., C.W. Recksiek and M.H.
Prager. 1988. Basic fishery science programs: a compendium
of microcomputer programs and manual of operation. Elsevier Science Publishing
Co., New York. 230 p.
Sprugel, D.G. 1983. Correcting for bias in log-transformed
allometric equations. Ecology 64(1):209-210.
Torres,
F. Jr. 1991. Tabular data on marine fishes from
Southern Africa, Part I. Length-weight relationships. Fishbyte 9(1):50-53.
Vakily, J.M., M.L. Palomares and D. Pauly. 1986. Computer programs for fish stock assessment: applications for the HP41 CV calculator. FAO Fish. Tech. Pap. 101 Suppl. 1, 255 p. Rome.
Crispina
Binohlan e Daniel Pauly
A informação desta tabela é necessária no cálculo da avaliação de
stocks
Esta tabela contém informação sobre crescimento, mortalidade
natural e o comprimento até à primeira maturação, que são dados importantes na
produção de modelos para a avaliação de stocks. Estes dados podem ainda ser
utilizados na produção de relações empíricas entre os parâmetros de crescimento
ou no cálculo de mortalidade natural e dados correlacionados (forma do corpo,
temperatura, etc), que configuram uma linha de investigação útil para a
avaliação dos stocks e também para conhecer melhor a evolução das estratégias
biológicas (Fig. 13).
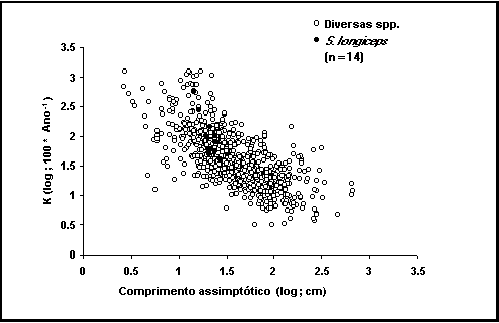
Fig.
13. Gráfico auxiométrico para Sardinella longiceps e para 20%
dos dados de outras espécies.
Os parâmetros de crescimento incluídos nesta tabela
são os de von Bertalanffy (VBGF; von Bertalanffy 1938), que têm a fórmula:
Lt =L¥ (1- e-k
(t-t0)) …1)
Onde Lt
é o comprimento médio dum exemplar duma dada espécie com a idade t, L¥ é o seu comprimento médio assiptótico, isto é, o
comprimento que atingiram numa idade avançada, K é um factor de dimensão tempo-1, e t0 é a “idade teórica” (e
geralmente negativa) que teria com o comprimento zero.
Em semelhança, o VBGF para o crescimento em peso tem
a fórmula
Wt =W¥ (1-e -k
(t-t0)) b
…2)
Onde Wt
e W¥ são os pesos
correspondentes a Lt e L¥,
respectivamente, e b é o expoente de
relação comprimento-peso da fórmula
W=a.Lb
…3)
A tabela POPCRESCIMENTO inclui registos para os
quais, pelo menos, L¥ e K ou W¥ e K estão disponíveis, isto é, t0 pode não existir (este
parâmetro não biológico não é utilizado na maior parte dos modelos de avaliação
de stocks).
Fontes A
tabela contém, presentemente,
cerca de 4.600 parâmetros de crescimento calculados para mais de 1.150
espécies, extraídas de cerca de 2.000 fontes primárias e secundárias. As
compilações de Pauly (1978, 1980) contribuíram com cerca de 1/3 das entradas.
Campos Complementando
a MainRef uma DataRef é dada para cada grupo de parâmetros de crescimento, porque
frequentemente os parâmetros de crescimento são apresentados em artigos que não
fornecem os dados de onde os resultados provêm. Os “dados da fonte”, como
indicado por um campo de escolha, consistem em: anéis dos otólitos, anéis das
escamas, outros anéis anuais, anéis diários dos otólitos, marcação/recaptura,
frequência de comprimento, observações directas, vários tipos de dados, outros.
As secções Material e Métodos estão transcritas
Também o Método usado no cálculo é dado através
da selecção num campo de escolhas com os seguintes itens: Ford-Walford; von
Bartalanffy/Beverton; Gulland and Holt; regressão não linear; ELEFAN I;
outro(s) métodos.
A
avaliação doutros métodos, as suas exigências, bias e outras necessidades dos dados podem ser consultados em
Ricker (1975), Gulland (1983), Pauly (1984), Gayanilo et al. (1996) e outros textos sobre ciências das pescas.
Para
verificar o rigor dos parâmetros de crescimento incluímos:
a.
um campo de cálculo com
o índice de perfomance de crescimento N´ =log10k
+2log20L4 ; Pauly and Munro, 1984), que podem ser comparados
com os valores de N´de outros stocks da mesma espécie.
b.
um campo de escolha múltipla
descreve a forma como L¥
foi convertido em W¥,
com as seguintes escolhas:
·
Tal como dado para
crescimento em MainRef ou Ref.;
·
Calculado usando a
relação L/W do mesmo stock;
·
Calculado usando a
relação L/W de outro stock da mesma espécie;
·
Calculado utilizando a
relação L/W de espécies similares;
·
Outros (ver
Comentários)
c.
um campo sim/não é
usado para identificar os casos nos quais L4 difere da Lmax
(na tabela ESPÉCIES) em mais de 30% de Lmáx;
d.
um campo sim/não pode
ser utilizado para identificar pares duvidosos de parâmetros de crescimento (Lµ e K ou Wµ e K) pode ser o uso de grelhas auxiométricas, ou
seja, “plots” de logK versus logL4(ou W4) porque stocks diferentes da mesma espécie devem
formar distintos padrões elipsoides;
e.
um botão de gráfico na
tabela resumo que, quando se clica, mostra um gráfico do tamanho do corpo vs
idade relativa (Fig. 14) que pode ser utilizado para identificar curvas de
crescimento que estejam desviadas da tendência naormal;
f.
botões de gráfico que
mostram gráficos auxiométricos, por exemplo, plots de logK vs logL¥ (Fig. 13) ou W¥ (veja “Análises Auxiométricas”, neste volume).
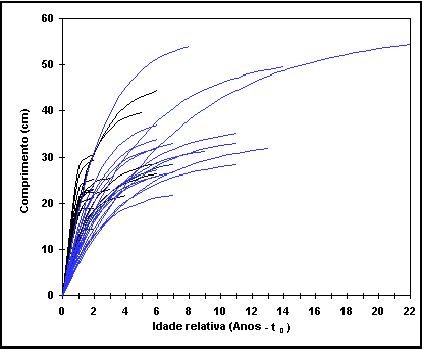
Fig. 14. Comprimento do corpo vs idade relativa (t-t0)
em Oreochromis
niloticus niloticus. As curvas são baseadas nos parâmentros L¥ and K da tabela POPCRESCIMENTO, e VBGF (Equação 1).
Informação do tamanho na primeira maturação sexual,
que aparece numa tabela separada (MATURAÇÃO), é usada em conjunção com L4 para computar a “capacidade reprodutora” (Cushing,
1981) da população, ou seja, a razão Lm/L4 . A maior parte dos valores Lm referem-se ao comprimento médio ou ao comprimento a
partir do qual 50% da população está sexualmente madura, mas sempre que estas
estimativas não são dadas, ou não possam ser conseguidas a partir dos dados, Lm foi tomado como o valor
médio de valores já publicados.
Para alguns registos, as estimativas L4 têm ainda de ser confrontadas com os registos dos
comprimentos máximos (Lmax)
os quais, acreditamos, devem estar razoavelmente próximos (ver acima).
Esperamos pelo “feedback” dos
utilizadores àcerca do conteúdo e/ou utilidade desta tabela.
Como chegar lá Clique
o botão Biologia na janela ESPÉCIES,
O BOTÃO Dinâmica de populações na
janela BIOLOGIA, e o botão Crescimento
na janela DINÂMICA DE POPULAÇÕES.
Referências Cushing, D.H. 1981. Fisheries biology: a
study in population dynamics. 2nd ed. University of Wisconsin Press,
Madison. 295 p.
Gayanilo, F.C. Jr., P. Sparre and D. Pauly. 1996. The FAO-ICLARM Stock Assessment Tool (FiSAT). User's Guide. FAO
Comp. Inf. Ser./Fish. 7, 126 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic methods. FAO/Wiley, New York.
Pauly, D. 1978. A preliminary compilation of fish length
growth parameters. Ber. Inst. Meereskd. an der Christian-Albrechts
Univ. Kiel 55, 200 p.
Pauly, D. 1980. On the interrelationships between natural
mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish population
dynamics in tropical waters: a manual for use with programmable calculators.
ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and J.L. Munro. 1984. Once more on growth comparison in fish and
invertebrates. Fishbyte 2(1):21.
Ricker, W.E. 1975. Computation and interpretation of
biological statistics of fish populations. Bull. Fish. Res. Board Can. 191. 382 p.
von Bertalanffy, L. 1938. A quantitative theory of organic laws II.
Hum. Biol. 10:181-213.
Crispina Binohlan e Daniel Pauly
Na FishBase são utilizados os parâmentos da função de
crescimento de von Bertalanffy ou VBGF (von Bertalanffy Growth Function) (veja
a “tabela POPCRESCIMENTO”, neste volume) para descrever o crescimento dos
peixes. Contudo, isto não resolve por si só, o problema mencionado por Kinne
(1960) uma vez que nenhum destes parâmentros possui a unidade do crescimento
(i.e., comprimento vs tempo ou peso vs tempo). L¥ e W¥ representam apenas o tamanho, e K e t0
têm apenas a dimensão tempo-1 e tempo, respectivamente. No entanto,
várias combinações destes parâmentros, e.g., L¥. K, possuem uma dimensão adequada (l/t) da taxa de
crescimento (Gallucci and Quinn 1979). Apesar
da base logarítmica os índices de crescimento:
Ø’ = logK + 2logL¥ …1)
e
Ø = logK + (2/3)logW¥ …2)
têm a unidade correcta da taxa de crescimento e são
amplamente utilizados para comparar o crescimento de diversos peixes e invertebrados,
devido a estes terem uma distribuição normal para diferentes populações de uma
mesma espécie (veja, por ex., Moreau et al. 1986).
Esta última característica também permite estimar K a partir de L¥ ou W¥ quando a o seu Ø’ ou Ø (média) é conhecido a partir
de uma ou mais populações (Munro & Pauly 1983; Pauly
& Munro 1984).
Os declives de 2 e 2/3 nas Equações (1) e (2)
respectivamente, foram estimados por Pauly (1979) a partir de uma grande série
de dados documentados em Pauly (1978, 1979), e que são agora incluídos na
FishBase. A Equação (1) implica que que os gráficos de logK vs logL¥ tenham em média um declive igual a 2. Do mesmo modo,
a Equação (2) implica que os gráficos de logK vs logL¥ tenham em média um declive de 2/3.
Um gráfico auxiométrico (do Grego “crescimento” e
“medida”) é um gráfico do parâmentro K de VBGF vs tamanho assimptótico (L¥ or W¥), com ambos os eixos em escala logarítmica. Uma
população com uma série de parâmentros de crescimento (L¥, K or W¥ , K) é
representada por um único ponto, e diferentes populações da mesma espécie terão
tendência a formar um grupo (“cluster” ) de pontos. Uma vez que as equações (1)
e (2) implicam que a estes grupos de pontos possam ser ajustadas linhas de
regressão de declive conhecido, também aos grupos de pontos podem ser
sobrepostas elipses com eixos de declive 2 ou 2/3, respectivamente, com
intercepções iguais a Ø’ ou Ø, e áreas de superfície relacionadas com a variabilidade
dos dados representados.
O programa AUXIM estima a área de confiança de 95% para os
parâmentros de crescimento
Assim, elipses AAacuja circunferência contém 95% da área de confiança
(S95) de um cluster com valores L¥ , K (ou
W¥ , K) values,
podem ser rapidamente estimadas e foi desenvolvido um software (AUXIM),
descrito em Pauly et al. (1996), para
realizar estas funções em ficheiros que possuam pelo menos 4 pares de valores
de L¥ , K ou W¥ , K.
Como é aborrecido utilizar o AUXIM como aplicação
única, foram incluídas na FishBase parte das suas rotinas de modo a permitir a
análise dos diversos parâmetros de crescimento que este programa contém.
Contudo, para a comparação entre peixes de formas bastante diferentes, apenas estão
incluídas as rotinas relativas ao crescimento em peso (e Ø, mas não Ø’).
As análises auxiométricas que podem ser realizadas
dentro da FishBase dependem da localização na base de dados quando se pede
estas análises:
1) quando as rotinas auxiométricas são chamadas dentro
da janela Crescimento da População, é mostrado um gráfico de logK vs W¥ para todas
as espécies da FishBase com esses valores (a amarelo), os pontos da espécie
onde esta rotina foi pedida ( a vermelho), e uma elipse que define S95
(se o número de casos n > 4; veja Caixa 11). Além disso, se n >
4, será exibida uma tabela com dados sobre a eclipse (W¥ e K
médios);
2) quando as rotinas auxiométricas são chamadas a partir
do menú RELATÓRIOS, e foi identificada uma ordem, família, ou grupo de espécies
por ambiente; pode ser realizada uma análise auxiométrica completa que involve:
a) a representação da elipse para a
espécie seleccionada (veja a Caixa 11) e a estimativa dos seus valores médios
de K e W¥ (nos casos em que n < 4, as médias são obtidas sem
que a elipse seja mostrada), e a apresentação de um gráfico (Fig. 15) que
mostra as elipses e/ou as médias para todas as espécies seleccionadas;
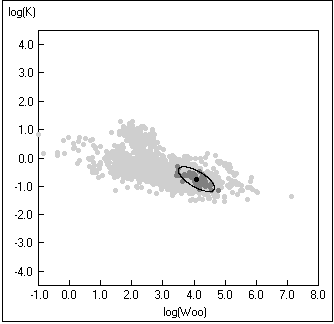
Fig. 15.
Gráfico de K vs W¥ . Os pontos
claros representam todas as espécies para as quais W¥ se encontra disponível na
FishBase, os pontos escuros representam as entradas para Gadus morhua. A elipse com um ponto preto no centro representa os
limites de confiaça de 95%. Consulte a Caixa 11.
c)
utilização das
distâncias de (b) e do algorítmo de agrupamento de McCammon &
Wenninger (1970) para
construir um dendograma das distâncias no “espaço crescimento” , ou seja,
mostrando as similaridades das espécies (pertencentes ao grupo seleccionado) em
relação ao seu crescimento (Fig. 16).
Caixa 11.
Antecedentes e utilização do AUXIM.
Esta
caixa resume as principais características do abordagem utilizada no AUXIM para
representar as elipses, tendo a primeira parte deste texto sido adaptada de
Pauly et al. (1996). Dado o peso VBGF
e a definição de Ø, temos
logK
= Ø - 2/3 logW¥
que
é a equação do eixo principal da elipse, em que Ø corresponde à intercepção na ordenada.
Ao
mesmo tempo, e uma vez que é perpendicular, a equação do eixo menor da elipse é
logK
= Y° + 3/2 logW¥
onde
Yo é a ordenada na origem O ponto de intercepção do eixo menor com a
abcissa é
Xo
= logW¥ - 2/3 logK
Se
uma elipse corresponde a uma nuvem de pontos com um limite de confiança de 95%,
o comprimento (2 · a) do eixo principal deve estar relacionado com o desvio
padrão de X°. Simultaneamente, o comprimento do eixo menor (2 · b)
deverá estar relacionado com o desvio padrão de Ø, ou
2
· a = 2 · t · sd(Xo) · 3/2 · 3/2 · (1/ ((1 + (3/2)2)1/2)
2
· b = 2 · t · sd(Ø) · 3/2 · 3/2 · (1/ ((1 + (3/2)2)1/2)
onde
o valor do teste-t se encontra relacionado com o número de pontos (n), com t =
1.96 quando n = ¥
(Sokal & Rohlf 1995); e onde o factor 3/2 · 3/2 · (1/ ((1 + (3/2)2)1/2)
entra em consideração com o facto de os eixos da elipse não serem paralelos aos
eixos do sistema de coordenadas.
Quando
as elipses se referem aos desvios padrão da média dos valores de logW¥ e logK, sd(Xo) e sd(Ø) são substituídas pelos erros padrão, ou seja, por se(Xo) e se(Ø), respectivamente.
Como utilizar o AUXIM:
A
interface do utilizador do AUXIM tem quatro partes:
1.
“Botões de comando” no canto
superior esquerdo do ecrã com funções para: (i) aumentar ou diminuir o tamanho
do gráfico auxiométrico (i.e. zoom-in e zoom-out); (ii) abrir a lista de
espécies seleccionadas antes de activar a rotina do AUXIM (apenas disponível
caso o AUXIM tenha sido aberto a partir do Menú Relatórios); e (iii) abrir a
tabela dos parâmetros de crescimento para as espécies em questão;
2.
Display
das espécies seleccionadas e dos botões de comando que permitem movimentar na
lista (canto superior direito);
3.
Display tab,
mostrando o gráfico auxiométrico e que também permite visualizar a tabela de
distância e sobreposição, tal como o dendograma; e
4.
Sistema de botões de
comando para: (i) seleccionar ou cancelar a seleecção de uma espécie da lista;
(ii) imprimir o ecrã ou gravar a
informação num ficheiro; (iii) abrir o ficheiro ajuda; ou (iv) fechar e
regressar à FishBase.
Repare
que as funções associadas com os botões de comando também podem ser efectuadas
clicando no botão direito do rato. Também pode seleccionar as espécies clicando
duas vezes na espécie e cancelar a selecção carregando na <Barra de
Espaços>.
Referências
Pauly, D., J. Moreau and F. Gayanilo, Jr. 1996. A new method for
comparing the growth performance of fishes, applied to wild and farmed
tilapias, p. 433-441. In R.S.V.
Pullin, J. Lazard, M. Legendre, J.B. Amon Kothias and D. Pauly (eds.) The Third
International Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Sokal, R.R. and F.J. Rohlf. 1995. Biometry. Third
edition. W.H. Freeman and Company, San Francisco. 887 p.
Daniel Pauly e Felimon
C. Gayanilo, Jr.
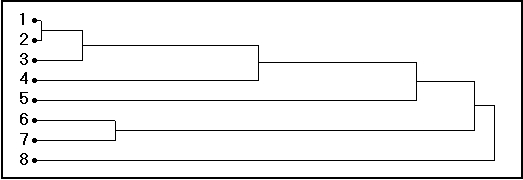
Fig. 16.
Dendograma AUXIM da similaridade no “espaço crescimento” para espécies da
família Gadidae, with 1= Theragra
chalcogramma; 2 = Trisopterus luscus;
3 = Merlangius merlangus; 4 = Micromesistius poutassou; 5 = Melanogrammus aeglefinus; 6 = Gadus morhua; 7 = Pollachius virens; 8= Trisopterus
minutus.
Até ao momento, estas análises têm sido apenas
efectuadas para tilápias, Fam. Cichlidae (Pauly et al. 1996) e peixes da Fam. Lutjanidae (Pauly &
Binohlan 1996), e o
seu potencial ainda não foi totalmente explorado. No entanto, cremos que estas
análises aumentarão consideravelmente o nosso conhecimento acerca do
crescimento, e da biologia dos peixes em geral, e gostariamos de saber a sua
opinião a este respeito.
Referências Gallucci, V.F. and T.J. Quinn, II. 1979. Reparameterizing,
fitting, and testing a simple growth model. Trans. Am. Fish. Soc. 108(1):14-25.
Kinne, O. 1960. Growth, food intake, and food consumption
in an europlastic fish exposed to different temperatures and salinities.
Physiol. Zool. 33:288-317.
McCammon, R.B. and G. Wenninger. 1970. The dendrograph. Computer Contribution 48.
State Geological Survey. The University of Kansas, Lawrence. 26 p.
Moreau, J., C. Bambino and D. Pauly. 1986. A comparison of four indices of overall fish
growth performance, based on 100 tilapia populations (Fam. Cichlidae), p.
201-206. In J.L. Maclean, L.B. Dizon
and L.V. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries
Society, Manila, Philippines.
Munro, J.L. and D. Pauly. 1983. A simple method for comparing the growth of
fishes and invertebrates. Fishbyte 1(1):5-6.
Pauly, D. 1978. A
preliminary compilation of fish length growth parameters. Ber. Inst. Meereskd.
Christian-Albrechts-Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill
size and temperature as governing factors in fish growth: a generalization of
von Bertalanffy’s growth formula. Ber. Inst. Meereskd.
Christian-Albrechts-Univ. Kiel 63, 156
p.
Pauly, D. and J.L.
Munro. 1984. Once more on the comparison of growth in fish
and invertebrates. Fishbyte 2(1):21.
Pauly, D. and C.
Binohlan. 1996. FishBase and AUXIM as tools for comparing the
life-history patterns, growth and natural mortality of fish: applications to
snappers and groupers, p. 223-247. In
F. Arreguin-Sánchez, J.L. Munro, M.C. Balgos and D. Pauly (eds.) Biology,
fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. 48.
Pauly, D., J. Moreau and F.
Gayanilo, Jr. 1996. A new method for comparing the growth
performance of fishes, applied to wild and farmed tilapias, p. 433-441. In R.S.V. Pullin, J. Lazard, M.
Legendre, J.B. Amon Kothias and D. Pauly (eds.) The Third International
Symposium on Tilapia in Aquaculture. ICLARM Conf. Proc. 41.
Daniel Pauly, Jacques Moreau e
Felimon Gayanilo, Jr.
Em biologia das pescas, a mortalidade é usualmente
expressa como taxas instantâneas, assim:
N0=N1 ÿ e (-z · t )
onde
N0 e N1 são os números sucessivos duma população afectada
pela taxa de mortalidade (total) Z, durante
o intervalo de tempo t.
Sumariamente temos:
Z=F + M
onde F é a
mortalidade por pesca e M é a
mortalidade natural, causada por qualquer outro factor que não a pesca (num
stock não explorado Z=M,
obviamente).
Foram incorporadas todas as estimativas de mortalidade natural bem
documentadas
Estimativas de
mortalidade natural são difíceis de obter (excepto em populações não exploradas,
que tendem a ser inacessíveis para o estudo, e são cada vez mais raras). Assim,
toda a estimativa de M bem
documentada na literatura foi incorporada na tabela POPCRESCIMENTO, que inclui
agora mais de 400 estimativas de mortalidade natural, de mais de 200 espécies
(ver Caixa 12). Cerca de 42% destas estimativas são de Pauly (1980; veja
“Análise da Produção-por-recruta”) enquanto que 21% são de Beverton and
Holt (1959) e de Djabali et al. (1993) .
É de notar que estes resultados são independentes, isto é não foram calculados usando modelos
empíricos, ligando valores de M a
variáveis incorrectas, como é explicado por Pauly (1980). Assim, as estimativas
de M apresentadas, podem ser
utilizadas para construir novos modelos empíricos.
Como ajuda, a temperatura média ambiental (em 0C)
foi adicionada ao registo POPCRESCIMENTO que inclui a estimativa M. Também o método de cálculo de M está registado, como uma das
seguintes escolhas: curva de capturas num stock não explorado; comprimento
médio dos indivíduos do stock não explorado; marcação-recaptura; “plot” de Z no esforço de pesca; “plot”
parabólico de Z na captura; Ecopath
modelo trófico (Christensen and Pauly 1993); outro método.
Estas técnicas são descritas nos livros de texto
indicados na tabela POPCRESCIMENTO, com excepção das envolvidas no modelo
Ecopath, descrito na Caixa 14.
Caixa 12. Mortalidade
natural dos peixes.
Os dados de mortalidade natural da FishBase são
baseados naquela que é seguramente a maior compilação de estimativas de
mortalidade natural em todo o mundo, isto é, não existem dados similares que
possam ser utilizados para verificar as generalizações obtidas a partir desta
série de dados. Deste modo, uma vez que é difícil obter replicação independente
dos nossos resultados, deveremos ser cuidadosos na apresentação de
generalizações baseadas nesta série de dados.
Assim, limitámo-nos a apresentar dois gráficos que
confirmam generalizações anteriores de Beverton and Holt (1959) e Pauly (1980). O
primeiro destes gráficos (Fig. 17) é um
gráfico do logM vs logK, os
parâmetros da equação de crescimento de von Bertalanffy. Confirma-se que K, que está relacionado com a
longevidade, é um bom indicador de M. No entanto, a variância é elevada o que
sugere que também outros factores podem influenciar M.
O segundo gráfico (Fig. 18) representa dois dos
factores que influenciam M: tamanho e temperatura ambiental. Os pontos são
estimativas de logM vs estimativas
correspondentes logL¥; os pontos a preto representam as estimativas para temperaturas acima
de 17°C (cerca de 50% de todos
os casos) e os pontos brancos para as restantes.
Como é possível ver no gráfico, M está não só
relacionado com L¥ (e com K; veja Fig. 17), mas também com a temperatura.
Referências
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and
mortality rates of fish in nature and their relation to growth and other
physiological characteristics, p. 142-180. In
G.E.W. Wolstenholme and M. O'Connor (eds.) CIBA Foundation Colloquia on Ageing:
the lifespan of animals. Vol 5, J. & A. Churchill Ltd., London.
Charnov, E. 1993. Life-history invariants: some
explorations of symmetry in evolutionary ecology. Ecology and Evolution. Oxford
University Press, Oxford. 128 p.
Pauly, D. 1980. On the
interrelationships between natural mortality, growth parameters, and mean environmental
temperature in 175 fish stocks. J.
Cons. CIEM 39(2):175-192.
Daniel
Pauly
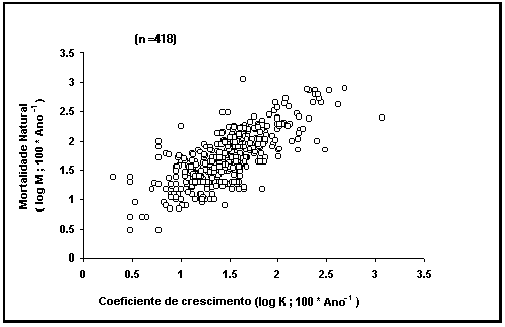
Fig. 17.
Mortalidade natural vs coeficiente de
crescimento para todos os peixes com dados disponíveis. Consulte a Caixa 12.
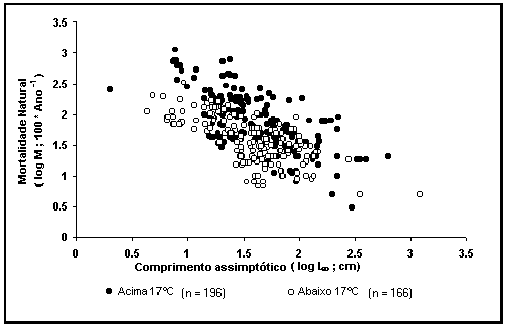
Fig. 18
Mortalidade natural vs comprimento
assimptótico para os peixes com dados disponíveis. Veja o efeito da temperatura
e consulte a caixa 12
Referências
Beverton, R.J.H. and S.J. Holt. 1959. A review of the lifespans and mortality rates of fish in
nature and their relation to growth and other physiological characteristics, p.
142-180. In G.E.W. Wolstenholme and
M. O'Connor (eds.) CIBA Foundation Colloquia on Ageing: the lifespan of
animals. Vol. 5, J. & A. Churchill Ltd., London.
Christensen, V. and D. Pauly, Editors. 1993. Trophic models of aquatic
ecosystems. ICLARM Conf. Proc. 26, 390 p.
Djabali, F., A. Mehailia, M. Koudil and B. Brahmi. 1993. Empirical equations for the estimation of
natural mortality in Mediterranean teleosts. Naga, ICLARM Q. 16(1):35-37.
Pauly, D. 1980. On the interrelationships between natural
mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Daniel
Pauly e Crispina Binohlan
Análises
de Produção-por-recruta
Uma das
razões principais que leva os cientistas a estudar o crescimento dos peixes e a
descrevê-lo através da função de crescimento de von Bertalanffy (VBGF), é para
fazer avaliações de stocks utilizando o modelo de Produção-por-recruta (Y/R) de
Beverton & Holt (1957) ou uma das suas variantes.
Assim, para
optimizar o uso dos parâmetros VBGF na FishBase 97, foi incluído um botão Y/R na tabela POPCRESCIMENTO que,
quando pressionado, possibilita a a realização de diversas análises de
Pordução-por-recruta, de acordo com as entradas da tabela e as escolhas do
utilizador. Para ver as definições de alguns dos termos utilizados abaixo,
consulte os capítulos sobre a tabela POPCRESCIMENTO, Mortalidade Natural e a
tabela COMPRIMENTO-PESO.
Recrutas são os
juvenis que a partir de um determinado tamanho entram na fase explorada
Antes de apresentar
as opções disponíveis devem ser definidos os termos “recruta” e
“produção-por-recruta”. Apesar de a definição variar de acordo com os autores,
podemos neste caso considerar como recrutas os juvenis vuneráveis à pesca, cujo
crescimento é descrito pela equação VBGF e cuja taxa instantânea de mortalidade
natural é semelhante à dos adultos. Estes recrutas têm uma idade média tr,
um comprimento médio Lr e um peso médio Wr. Quando
alcançam a idade tr, os recrutas podem ser capturados imediatamente,
caso em que a idade da primeira captura iguala a idade do recrutamento (tc
= tr). Por outro lado, os recrutas podem ser capturados numa idade
mais avançada (com um tamanho superior correspondente, Lc e Wc).
Neste caso, devido à mortalidade natural, o número de recrutas que entram na
fase explorada Rr será inferior do que o número de recrutas inicial
Rc, ou
![]() …1)
…1)
Deste
modo, para cada combinação de valores tc e F, existe uma
produção-por-recruta (Y/R = captura em peso, por recruta) que pode ser estimada
a partir de várias equações cuja forma específica depende do modelo utilizado
para descrever o crescimento do peixe. Nos parágrafos seguintes, são dadas as
equações para a estimativa de Y/R segundo três formas de VBGF, isto é,
ou VBGF
padrão, com base na conversão de comprimento utilizando a relação
comprimento-peso
![]() …3)
…3)
onde c.f.
é o factor condição.
Modelo original de Beverton e Holt
Caso II: ![]() …4)
…4)
que é uma forma
especial de VBGF onde o expoente (b) da relação comprimento-peso pode tomar
valores diferentes de 3, isto é,
![]() …5)
…5)
onde b ¹ 3
Caso III: ![]() …6)
…6)
que
representa o crescimento em comprimento VBGF, e que pode ser utilizada para a
análise relativa de produção-por-recruta quando a relação comprimento-peso não
está disponível.
Estimativa da produção-por-recruta
O Caso I é
o modelo original de Beverton and Holt (1957), que têm a formula:
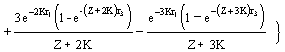 …7)
…7)
r1 = tc - t0;
r2 = tc - tr;
r3 = tmax – tc;
e
onde L¥ , K e t0 são
parâmetros de crescimento (veja a tabela “POPCRESCIMENTO”, neste vol.), a
definição de tc e tr é a mencionada acima e tmax
é “a idade máxima de contribuição para a fase explorada” (Ricker 1975) ou, de
forma mais simples, a longevidade do peixe em questão (tal como apresentado na
tabela ESPÉCIES). O efeito do valor exacto de tmax
é geralmente pequeno, e assim, quando não é possível encontrar um valor elevado
e adequado de tmax, a Equação (7) pode ser consideravelmente
simplificada fazendo tmax = ¥, neste caso a Equação (7) fica:
![]() …8)
…8)
sendo os
parâmetros os indicados na Equação(7).
Ambas as
equações (7) e (8) podem ser utilizadas para estimar o efeito na
produção-por-recruta, de diferentes valores de tc, correspondentes a
diferentes valores de Lc , tais como os causados por redes de
diferentes tamanhos, e em que F corresponde a diferentes intensidades de pesca.
A rotina
gráfica aqui incluída permite visualizar e imprimir dois tipos de gráficos: (a)
gráficos Y/R (sempre em g × ano-1) vs F (ano-1),
para valores de Lc seleccionados pelo utilizador (Fig. 19), ou (b)
“gráficos de isopletas”, que apresentam a produção-por-recruta para valores de
Lc/L¥ que variam entre 5 e 95% de L¥ , e valores de F desde zero até um limite
superior (po defeito 5 ano-1; max. = 20 ano-1) escolhido
pelo o utilizador (veja a Fig. 20, e a Caixa 13).

Fig. 19. Gráfico bi-dimensional de
produção-por-recruta para Plectropomus leopardus. Os parâmetros utilizados são: W¥ = 2,220 g; K = 0.43 ano-1;
to = 0.34 anor-1, M = 0.86 ano-1; b = 3.2; tr
= 0.12; e tmax = 26 anos. Veja a Caixa 13.

Fig. 20. Gráfico
tri-dimensional das isopletas de produção-por-recruta para Plectropomus leopardus em função do tamanho relativo no início da fase explorada Lc/L¥
e da mortalidade. Os parâmetros utilizados são: L¥ = 45 cm; M/K = 2; tc = 0.12
ano; tmax = 26 anos; e Lc = 20 cm. Consulte a Caixa 13.
Caixa
13. Gráficos de produção-por-recruta
(Y/R) e biomassa-por-recruta (B/R) .
A
rotina Y/R incluída na FishBase é construída de modo a que os gráficos Y/R e
B/R sejam apresentados mesmo que apenas estejam disponíveis na tabela
POPCRESCIMENTO os valores de L¥ e K. Isto é, são fornecidos por defeito para os
parâmetros em falta do seguinte modo:
O
Caso I (veja Análise de Produção-por-recruta, neste volume) aplica-se quando W¥ está disponível e b = 3. O gráfico inicial assume tr
= 0, t0 = 0 (se estes valores não estiverem disponíveis na tabela
POPCRESCIMENTO), e Lc = 0.05 × L¥. O valor de M é tratado como no Caso III, exepto na
Equação (10) que fornece uma estimativa de M. Os parâmetros tr e t0
podem ser posteriormente alterados, o primeiro introduzindo um valor de Lr
(modificado internamente em tr), e o segundo introduzindo um valor
escolha, ou uma estimativa aproximada, obtida através da equação
log(-t0)
» -0.3922 - 0.2752 logL¥ - 1.038 logK
onde
L¥ está em cm (TL),
e K em ano-1, e que é baseada em 153 tripletos de valores de t0
, L¥ e K seleccionados de Pauly (1978) de modo a cobrir a grande diversidade
de taxa e tamanhos dos peixes (Pauly
1979). Na Equação (7) o valor de tmax é obtido a partir da tabela
ESPÉCIES quando está disponível, caso contrário tmax = ¥ e é utilizada a Equação (8).
O
Caso II é utilizado quando W¥ está disponível e b = 3; t0, tr,
Lc e M são tratados como no Caso I.
O
Caso III aplica-se quando W¥ não está disponível e tem que se utilizar L¥. É
assumido que b = 3, t0 = 0, tmax = ¥ , tr = 0, e Lc = 0.05 × L¥. São fornecidas rotinas para entrada de valores de M
diferentes do “default”, estabelecido para M = 2K (é fornecida uma rotina que
utiliza a Equação (9), ou seja, é necessário introduzir T em °C), e vários Lc;
Os
gráficos de biomassa/recrutamento apresentados juntamente com a análise Y/R
baseiam-se em versões modificadas das Equações (7), (8) e (12) e devem ser
tomados em consideração quando se interpretam os gráficos Y/R (ver abaixo).
Os
gráficos aparecem em dois modos: (1) 2D, com as formas de Y/R e as linhas B/R
dependendo de Lc; e (2) 3D, isto é, como diagramas da produção
(biomassa) em isopletas. Os primeiros gráficos mostram três pontos de
referência:
·
Emax ou Fmax
, i.e., o valor de E ou F associado com
o maior valor possível de Y/R para um dado valor de Lc ;
·
E0.1 e F0.1,
o valor de E ou F para o qual o declive
de Y/R é 1/10 do seu valor na origem; e
·
E0.5 e F0.5
, os valores de E ou F relacionados com uma redução de biomassa (por
recruta) de 50% no stock inexplorado.
Estes
pontos de referência, que correspondem às três linhas verticais tracejadas da
Fig. 19, são discutidos na parte final da secção “Análise de
Produção-por-recruta”.
Referências
Pauly, D. 1978. A preliminary
compilation of fish length growth performance. Ber. Inst. Meereskd.
Christian-Albrechts-Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish
growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst.
Meereskd. Christian-Albrechts-Univ. Kiel 63, 156 p.
Daniel Pauly
Em todas estas análises o valor de M é retirado da
tabela POPCRESCIMENTO (veja secção sobre Mortalidade Natural), introduzido pelo
utilizador, ou gerado apartir das equações empíricas de Pauly (1980), as quais
assumem a seguinte forma para o
comprimento
LogM = -0.066-0.279logL¥+0.6543logK+0.4634logT …9)
e para o peso
LogM = -0.2107-0.0824 logW¥+0.6757logK+0.4627logT …10)
onde M e K são expressos numa base anual, L¥ e W¥ são expressos em cm (TL) e g (peso fresco)
respectivamente, e onde T representa a
temperatura média ambiental (água) em °C. [Uma rotina interna converte valores baixos de T
(até 2°C) no seu equivalente
fisiológico mais alto (Pauly 1980); uma outra rotina converte os valores de L¥,
primeiramente expressos como SL ou FL, em TL de modo a que possam ser
utilizados na Equação (9); outras medidas de crescimento (WD, OT ou NA) são
deixadas inalteradas.]
Os parâmetros W¥ e K são
sempre retirados da tabela POPCRESCIMENTO, juntamente com t0, quando
disponível. Uma rotina permite introduzir valores de Lr e t0
acima do seu zero (veja Caixa 13).
Repare que Lr deverá permanecer £50% de L¥.
As Equações
(7) e (8) acima descritas assumem que o crescimento em peso é isométrico (i.e.
b = 3). Este pressuposto é muitas vezes desajustado da realidade variando
geralmente o valor de b, em relações comprimento-peso, entre 2.5 e 3.5 (veja
“tabela COMPRIMENTO-PESO”, neste volume). Um método possível para lidar com
valores de b ¹ 3 é
recorrer ao uso da função incompleta b, tal como
proposto por Jones (1957).
Aqui, a produção-por-recruta, quando tmax
= ¥, é dada por
![]() …11)
…11)
onde X = e-Kr1;
P = Z/K:
Q = b + 1;
b = é o símbolo
da função imcompleta beta, e r1 e r2 são definidos tal
como na Equação (7).
A rotina Y/R da FishBase
verifica automaticamente se b = 3. Se b não for igual a 3 é utilizada a Equação
(11) (veja Caixa 13). Por outro lado,
os parâmetros utilizados são os mesmos do que na Equação (8).
Caso III
Quando os parâmetros de uma relação comprimento-peso
não estão disponíveis, ainda é possível efectuar uma análise Y/R, utilizando o
conceito de pordução-por-recruta relativa (Y’/R) de Beverton and Holt
(1964) definido por
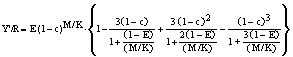 …12)
…12)
onde c = Lc/L¥ , e a taxa
de exploração é definida por E = F/Z.
Repare que a relação entre Y/B e Y/R é dada,
![]() …13)
…13)
enquanto que a relação
entre F e E é dada por
![]() …14)
…14)
Note também que a escala de E não é linear, com E = 1 correspondendo a F = ¥. Assim, valores
elevados de E indicam níveis de esforço insustentáveis, se não praticamente
impossíveis.
A
utilização de modelos de produção-por-recruta: AVISOS
É assumido que não
existe relação stock-recrutmento
Apesar de ainda adaptados à
gestão de certos stocks, os modelos de produção-por-recruta devem ser utilizados
com precaução. Os pescadores não estão interessados numa produção-por-recruta imaginária mas antes numa
produção material de peixe, e esta
corresponderá à produção-por-recruta multiplicada pelo número absoluto de
peixes produzidos no stock. A produção só
é directamente proporcional à produção-por-recruta, para uma grande variação de
mortalidades de pesca, se for assumido que não existe relação — para uma ampla
gama de valores de F ou E — entre o tamanho do stock parental e a sua
descendência (o que não é verdade, veja a tabela “RECRUTAMENTO”).
Devido ao pressuposto de equilíbrio, apenas se prevêm efeitos a
longo prazo
Assim, os valores de F ou de E necessários para
produzir um máximo de produção-por-recruta terão tendência a gerar valores de produção
extremamente baixos, porque Fmax e Emax reduzem o stock
parental a um nível em que são produzidos poucos recrutas. Além
disso, deve ser compreendido que a descoberta das análises de
produção-por-recruta só se aplicam a situações
de equilíbrio a longo prazo. A curto prazo, um aumento da mortalidade de
pesca ou uma diminuição no tamanho na captura resulta sempre em produções mais
elevadas, mesmo quando a análise prevê valores baixos. Do mesmo modo, uma
diminuição na mortalidade de pesca ou um aumento no tamanho da primeira captura
resulta sempre em produções mais baixas a curto prazo, apesar de, com o
decorrer do tempo, se alcançar produções mais elevadas. A duração do período de
transição pode ser de vários anos em peixes com grande longevidade e que estão
sujeitos a exploração há muitos anos, tal como o bacalhau. Em peixes com menor
longevidade, o período de transição será mais pequeno. No caso dos peixes com
período de vida muito curto, a distinção entre efeitos de curto e longo prazo
nem se aplica, uma vez que os stocks nunca estão em equilíbrio.
Devido ao pressuposto de equilibrio, apenas são previstos efeitos a
longo prazo
A análise Y/R para peixes tropicais pode ser muito enganadora
Uma outra importante
característica da análise de produção-por-recruta é o facto de esta ser
maximizada para valores baixos de E e F, apenas no caso de peixes de grandes
dimensões e longevidade, e com fraca mortalidade. Em pequenos peixes tropicais,
com valores de M elvados, os valores de E e F que maximizam a
produção-por-recruta são normalmente altos. Assim, pode ser muito muito
enganadora a gestão de pescas tropicais baseada apenas na análise Y/R para
espécies de peixes de pequena dimensão. [Esta nota ignora o bias adicional
devido à noção de recrutamento e selecção irregular implicita nas Equações (7), (8) e (12); veja Pauly and Soriano 1986, e
Silvestre et al. 1991]
Por esta e
outras razões, surgiu um acordo (arbitrário) para limitar F ao ponto onde o
declive da curva de produção-por-recruta tem 1/10 do seu valor na origem
(Gulland and Boerema 1973). Este
conceito, denominado F0.1, pode ser visto como um substituto para
MEY (Produção Económica Máxima), aplicável em situções onde não existem dados
sobre o desempenho das pescas. Um conceito análogo ao F0.1, mas
aplicável à taxa de Exploração E é E0.1, e é utilizado em conjunção
com o Caso III descrito acima.
Uma outra
salvaguarda quando se efectua uma análise Y/R é examinar sempre a curva de
biomassa-por-recruta correspondente (B/R or B’/R), que é calculada juntamente
com a pordução-por-recruta (obtem-se B/R dividindo Y/R por F, veja, por ex., a
Equação 8). O ponto de referência apropriado é o valor F (ou E) que reduz B/R
(ou B’/R) a metade do seu nível inexplorado (quando F ou E = 0), i.e., ao nível
de biomassa que maximiza a produção Supérfula gerando assim MSY (cf. Schaefer 1954, 1957;
Gulland 1983; or
Pauly 1984). Este valor é aqui referido como F0.5 ou E0.5.
Como chegar lá
Clique o botão Biologia
na janela ESPÉCIES, o botão Dinâmica de
Populações na janela BIOLOGIA, o botão Crescimento
na janela DINÂMICA DE POPULAÇÕES e, depois de seleccionar uma análise, o botão
Y/R na tabela CRESCIMENTO.
[Esta rotina só estará acessível se correr a FishBase
em Windows 95 ou NT.]
Referências
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish
populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Beverton, R.J.H. and S.J. Holt. 1964. Table of yield functions for fishery management.
FAO Fish. Tech. Pap. 38, 49 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic
methods. FAO/Wiley, New York.
Gulland, J.A. and L. Boerema. 1973. Scientific advice on catch levels. Fish.
Bull. (US) 71:325-335.
Jones, R. 1957. A much simplified version of the fish
yield equation. Doc. No. P. 21. Paper presented at the Lisbon joint meeting of
International Commission Northwest Atlantic-Fisheries, International Council
for the Exploration of the Sea, and Food and Agriculture Organization of the
United Nations. 8 p. (Mimeo).
Pauly, D. 1980. On the
interrelationships between natural mortality, growth parameters, and mean
environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish
population dynamics in tropical waters: a manual for use with programmable
calculators. ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and M.
Soriano. 1986. Some practical extensions to Beverton and
Holt’s relative yield-per-recruit model, p. 491-495. In J.L. Maclean, L.B. Dizon and L. Hosillos (eds.) The First Asian
Fisheries Forum. Asian Fisheries Society, Manila.
Ricker, W.E. 1975. Computation and interpretation of
biological statistics of fish populations. Bull. Fish. Res. Board Can. 191, 382
p.
Schaefer, M.B. 1954. Some aspects of the dynamics of
populations important to the management of the commercial marine fisheries.
Inter-Am. Trop. Tuna Comm., Bull. 1(2):27-56.
Schaefer, M.B. 1957. A study
of the dynamics of the fishery for yellowfin tuna in the eastern tropical
Pacific Ocean. Inter-Am. Trop. Tuna Comm., Bull. 2:247-268.
Silvestre, G., M. Soriano and D. Pauly. 1991. Sigmoid selection and the Beverton and Holt
equation. Asian Fish. Sci. 4(1):85-98.
Daniel Pauly e Felimon C. Gayanilo,
Jr.
As flutuações no recrutamento e as suas causas,
representam uma das áreas chave da investigação em pescas. Este facto não é de
todo surpreendente se pensarmos que estas flutuações determinam os níveis de
captura atingidas pelas frotas de pesca.
Não é possível
prevêr o recrutamento
É geralmente impossível prever o recrutamento futuro.
No entanto, generalizações grosseiras são possíveis (por ex., um stock
sobreexplorado produz menos recrutas do que outro menos explorado), e quanto
mais informação houver a este respeito das mais variadas regiões, mais precisas
e seguras serão estas generalizações.
Assim, foi extraordinário que R. A. Myers tenha
disponibilizado, para incluir na FishBase, a base de dados de recrutamento (e
toda a informação relacionada), que ele e a sua equipa do North West Atlantic
Fisheries Center, Science Branch, Department of Fisheries and Oceans, St.
John’s, Canada penosamente reuniram (Myers et
al., 1990, 1995). Salvo uma melhor explicação por R.A. Myers (agora na
Universidade Dalhousie, Halifax, Canadá), os próximos parágrafos descrevem,
sucintamente, a Tabela que criámos para alojar toda essa informação.
A tabela RECRUTAMENTO listará, em primeiro lugar,
para a espécie considerada, os stocks para os quais existe informação numa série
de recrutamento (e séries associadas, se houver). Clicando duas vezes nesse
stock acederá à tabela RECRUTAMENTO, propriamente dita.
Campos
O método usado para derivar as séries de recrutamento
(ou as relacionadas) é mostrado através de um campo de escolha múltipla com as
seguintes entradas:
1. contagens directas
2. informação esforço/captura
3. pesca-eléctrica
4. marcação-recaptura
5. SPA (VPA)
6. restabelecimento do stock
7. vigilância científica
8. ver informação adicional
São
indicadas também as cohortes utilizadas para estimar a mortalidade. Finalmente, toda a informação
restante desta base de dados encontra-se num campo concatenado, com todas as
entradas escritas após os cabeçalhos das colunas.
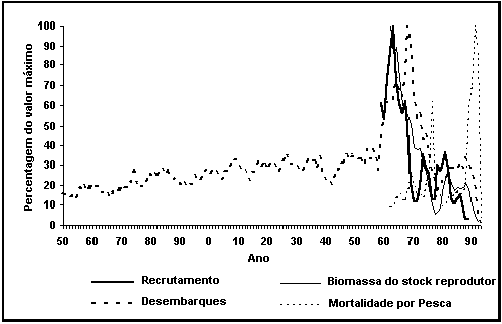
Se
clicar os botões gráfico ou tabela acederá a toda a informação do
recrutamento e, se existentes, às estimas de desembarque, à biomassa do stock
reprodutor e/ou à mortalidade por pesca. Note, contudo, que no gráfico, as
séries são expressas em unidades relativas (cada uma como % do seu valor
máximo) (veja Fig. 21), isto é, as entradas numéricas das séries devem ser
consultadas para obter os valores absolutos.
Fig. 21. Séries temporais de desembarque, biomassa do stock
reprodutor, recrutamento e mortalidade de pesca de bacalhau proóximo de
Newfoundland, Canada. Repare como a exploração moderna destruíu a pesca que
durante tanto anos foi sustentada.
Estão disponíveis
mais de 500 séries temporais de
recrutamento
Também pode aceder a
um gráfico que permite comparar a variabilidade das séries temporais de
recrutamento disponíveis, enquanto outro gráfico (Fig. 22) ilustra a relação
entre o tamanho do stock parental e recrutamento subsequente.
Presentemente, estão disponíveis mais de 500 séries
temporais de recrutamento para cerca de 120 espécies. Toda a actualização
passará por R. A. Myers, que deverá ser contactado directamente pelos
utilizadores interessados em contribuir (Myers@phys.ocean.dal.ca).
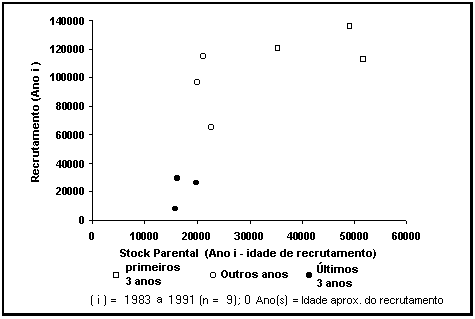
Fig. 22. Relação entre o
recrutamento e stock parental.
Como chegar lá
Clique o botão
Recrutamento na janela DINÂMICA DE
POPULAÇÕES.
Agradecimentos
Agradecemos a R. A. Myers e à sua equipa o
enriquecimento do Projecto FishBase com a sua valiosa base de dados.
Referências
Myers,
R. A., W. Blanchard and K. R. Thompson. 1990. Summary of North Atlantic fish
recruitment, 1942-1987. Can. Tech. Rep.
Fish.Aquat. Sci. No. 1743.
Myers,
R. A., J. Bridson and N. J. Barrowman. 1995. Summary of worldwide stock and
recruitment data. Can. Tech. Rep.
Fish.Aquat. Sci. No. 2024.
Daniel
Pauly e Crispina Binohlan